A se calculează conform următoarelor reguli:

Pentru concizie, folosiți |a|. Astfel, |10| = 10; - 1 / 3 = | 1 / 3 |; | -100| =100 etc.

Orice marime X corespunde unei valori destul de precise | X|. Si asta inseamnă identitate la= |X| stabileste la Ca unii funcția argument X.

Programa acest funcții prezentat mai jos.

Pentru X > 0 |X| = X, si pentru X< 0 |X|= -X; în legătură cu această linie y = | X| la X> 0 este aliniat cu linia y=x(bisectoarea primului unghi de coordonate) și când X< 0 - с прямой y = -x(bisectoarea celui de-al doilea unghi de coordonate).

Separa ecuații include necunoscute sub semn modul.

Exemple arbitrare de astfel de ecuații - | X— 1| = 2, |6 — 2X| =3X+ 1 etc.

Rezolvarea ecuațiilor care conține necunoscutul sub semnul modulului se bazează pe faptul că, dacă valoarea absolută a numărului necunoscut x este egală cu numărul pozitiv a, atunci acest număr x însuși este egal fie cu a, fie cu -a.

De exemplu: dacă | X| = 10, atunci sau X=10 sau X = -10.

Considera rezolvarea ecuațiilor individuale.

Să analizăm soluția ecuației | X- 1| = 2.

Să deschidem modulul apoi diferența X- 1 poate fi egal fie cu + 2, fie cu - 2. Dacă x - 1 = 2, atunci X= 3; dacă X- 1 = - 2, atunci X= - 1. Facem o substituție și obținem că ambele aceste valori satisfac ecuația.

Răspuns. Această ecuație are două rădăcini: X 1 = 3, X 2 = - 1.

Să analizăm rezolvarea ecuației | 6 — 2X| = 3X+ 1.

După extinderea modulului obținem: sau 6 - 2 X= 3X+ 1 sau 6 - 2 X= - (3X+ 1).

În primul caz X= 1, iar în al doilea X= - 7.

Examinare. La X= 1 |6 — 2X| = |4| = 4, 3X+ 1 = 4; rezulta din instanta X = 1 - rădăcină b dat ecuații.

La X = - 7 |6 — 2X| = |20| = 20, 3X+ 1= - 20; deoarece 20 ≠ -20, atunci X= - 7 nu este rădăcina acestei ecuații.

Răspuns. La ecuațiile au o singură rădăcină: X = 1.

Ecuaţiile de acest tip pot rezolva si grafic.

Deci haideți să decidem de exemplu, grafic ecuația | X- 1| = 2.

Să construim mai întâi graficul funcției la = |X— 1|. Să desenăm mai întâi graficul funcției. la=X- 1:

Acea parte a ei Arte grafice, care este situat deasupra axei X nu ne vom schimba. Pentru ea X- 1 > 0 și deci | X-1|=X-1.

Partea graficului care se află sub axă X, înfățișează simetric despre această axă. Pentru că pentru această parte X - 1 < 0 и соответственно |X - 1|= - (X - unu). Format ca urmare linia(linie continuă) și voință graficul funcției y = | X—1|.

Această linie se va intersecta cu Drept la= 2 în două puncte: M 1 cu abscisă -1 și M 2 cu abscisă 3. Și, în consecință, ecuația | X- 1| =2 va avea două rădăcini: X 1 = - 1, X 2 = 3.

Un modul este unul dintre acele lucruri despre care toată lumea pare să fi auzit, dar în realitate nimeni nu le înțelege cu adevărat. Prin urmare, astăzi va exista o mare lecție dedicată rezolvării ecuațiilor cu module.

Vă spun imediat: lecția va fi simplă. În general, modulele sunt în general un subiect relativ simplu. „Da, desigur, este ușor! Îmi face creierul să explodeze!” - vor spune mulți studenți, dar toate aceste rupturi de creier se datorează faptului că majoritatea oamenilor nu au cunoștințe în cap, ci un fel de porcărie. Și scopul acestei lecții este de a transforma prostiile în cunoștințe. :)

Un pic de teorie

Deci să mergem. Să începem cu cel mai important: ce este un modul? Permiteți-mi să vă reamintesc că modulul unui număr este pur și simplu același număr, dar luat fără semnul minus. Adică, de exemplu, $\left| -5 \right|=5$. Sau $\left| -129,5\right|=129,5$.

Este atât de simplu? Da, simplu. Care este atunci modulul unui număr pozitiv? Aici este și mai simplu: modulul unui număr pozitiv este egal cu acest număr însuși: $\left| 5\right|=5$; $\stânga| 129,5 \right|=129,5$ etc.

Se dovedește un lucru curios: numere diferite poate avea același modul. De exemplu: $\left| -5 \right|=\stânga| 5\right|=5$; $\stânga| -129,5 \right|=\left| 129,5 \right|=129,5 $. Este ușor de văzut ce fel de numere sunt acestea, în care modulele sunt aceleași: aceste numere sunt opuse. Astfel, observăm pentru noi înșine că modulele numerelor opuse sunt egale:

\[\stanga| -a \right|=\left| a\dreapta|\]

O alta fapt important: modulul nu este niciodată negativ. Orice număr luăm - chiar și pozitiv, chiar negativ - modulul său se dovedește întotdeauna a fi pozitiv (sau în cazuri extreme, zero). De aceea, modulul este adesea numit valoarea absolută a unui număr.

În plus, dacă combinăm definiția modulului pentru un număr pozitiv și negativ, obținem o definiție globală a modulului pentru toate numerele. Și anume: modulul unui număr este egal cu acest număr însuși, dacă numărul este pozitiv (sau zero), sau egal cu numărul opus, dacă numărul este negativ. Puteți scrie asta ca o formulă:

Există și un modul de zero, dar este întotdeauna egal cu zero. În plus, zero singular, care nu are opus.

Astfel, dacă luăm în considerare funcția $y=\left| x \right|$ și încercați să-i desenați graficul, veți obține un astfel de „daw”:

Exemplu de soluție pentru graficul modulului și ecuația

Din această imagine puteți vedea imediat acel $\left| -m \right|=\stânga| m \right|$, iar graficul modulului nu scade niciodată sub axa x. Dar asta nu este tot: linia roșie marchează linia dreaptă $y=a$, care, cu $a$ pozitiv, ne dă două rădăcini deodată: $((x)_(1))$ și $((x) _(2)) $, dar despre asta vom vorbi mai târziu. :)

Pe lângă o definiție pur algebrică, există una geometrică. Să presupunem că există două puncte pe dreapta numerică: $((x)_(1))$ și $((x)_(2))$. În acest caz, expresia $\left| ((x)_(1))-((x)_(2)) \right|$ este doar distanța dintre punctele specificate. Sau, dacă doriți, lungimea segmentului care leagă aceste puncte:

Modulul este distanța dintre punctele de pe dreapta numerică

De asemenea, din această definiție rezultă că modulul este întotdeauna nenegativ. Dar destule definiții și teorie - să trecem la ecuații reale. :)

Formula de bază

Bine, ne-am dat seama de definiție. Dar nu a devenit mai ușor. Cum să rezolvi ecuațiile care conțin acest modul?

Calm, doar calm. Să începem cu cele mai simple lucruri. Luați în considerare ceva de genul acesta:

\[\stanga| x\dreapta|=3\]

Deci modulo$x$ este 3. Cu ce ​​poate fi egal $x$? Ei bine, judecând după definiție, $x=3$ ne va potrivi foarte bine. Într-adevăr:

\[\stanga| 3\dreapta|=3\]

Mai sunt si alte numere? Cap pare să sugereze că există. De exemplu, $x=-3$ — $\left| -3 \right|=3$, adică egalitatea cerută este îndeplinită.

Deci, poate dacă căutăm, gândim, vom găsi mai multe numere? Și iată o pauză: mai multe numere Nu. Ecuația $\left| x \right|=3$ are doar două rădăcini: $x=3$ și $x=-3$.

Acum să complicăm puțin sarcina. Fie ca, în locul variabilei $x$, funcția $f\left(x \right)$ să atârnă sub semnul modulului, iar în dreapta, în loc de triplu, punem un număr arbitrar $a$. Obtinem ecuatia:

\[\stanga| f\stânga(x\dreapta) \dreapta|=a\]

Ei bine, cum te decizi? Permiteți-mi să vă reamintesc: $f\left(x \right)$ este o funcție arbitrară, $a$ este orice număr. Acestea. oricare! De exemplu:

\[\stanga| 2x+1 \dreapta|=5\]

\[\stanga| 10x-5 \dreapta|=-65\]

Să ne uităm la a doua ecuație. Poți spune imediat despre el: nu are rădăcini. De ce? Așa este: pentru că necesită ca modulul să fie egal cu număr negativ, ceea ce nu se întâmplă niciodată, deoarece știm deja că modulul este întotdeauna un număr pozitiv sau, în cazuri extreme, zero.

Dar cu prima ecuație, totul este mai distractiv. Există două opțiuni: fie există o expresie pozitivă sub semnul modulului și apoi $\left| 2x+1 \right|=2x+1$, sau această expresie este încă negativă, caz în care $\left| 2x+1 \right|=-\left(2x+1 \right)=-2x-1$. În primul caz, ecuația noastră va fi rescrisă astfel:

\[\stanga| 2x+1 \right|=5\Rightarrow 2x+1=5\]

Și dintr-o dată se dovedește că expresia submodulului $2x+1$ este într-adevăr pozitivă - este egală cu numărul 5. Adică, putem rezolva în siguranță această ecuație - rădăcina rezultată va fi o parte din răspuns:

Cei care sunt deosebit de neîncrezători pot încerca să înlocuiască rădăcina găsită în ecuația originală și să se asigure că va exista într-adevăr un număr pozitiv sub modul.

Acum să ne uităm la cazul unei expresii submodulului negativ:

\[\left\( \begin(align)& \left| 2x+1 \right|=5 \\& 2x+1 \lt 0 \\\end(align) \right.\Rightarrow -2x-1=5 \Săgeată la dreapta 2x+1=-5\]

Hopa! Totul este din nou clar: am presupus că $2x+1 \lt 0$ și, ca rezultat, am obținut că $2x+1=-5$ este într-adevăr expresia mai putin de zero. Rezolvăm ecuația rezultată, în timp ce știm deja cu siguranță că rădăcina găsită ne va potrivi:

În total, am primit din nou două răspunsuri: $x=2$ și $x=3$. Da, cantitatea de calcule s-a dovedit a fi puțin mai mare decât în ​​ecuația foarte simplă $\left| x \right|=3$, dar în principiu nimic nu s-a schimbat. Deci poate că există algoritm universal?

Da, un astfel de algoritm există. Și acum o vom analiza.

A scăpa de semnul modulului

Să ne dăm ecuația $\left| f\left(x \right) \right|=a$ și $a\ge 0$ (altfel, așa cum știm deja, nu există rădăcini). Apoi puteți scăpa de semnul modulo conform următoarei reguli:

\[\stanga| f\left(x \right) \right|=a\Rightarrow f\left(x \right)=\pm a\]

Astfel, ecuația noastră cu modulul se împarte în două, dar fără modul. Asta e toată tehnologia! Să încercăm să rezolvăm câteva ecuații. Să începem cu asta

\[\stanga| 5x+4 \right|=10\Rightarrow 5x+4=\pm 10\]

Vom lua în considerare separat când există un zece cu un plus în dreapta și separat când este cu un minus. Avem:

\[\begin(align)& 5x+4=10\Rightarrow 5x=6\Rightarrow x=\frac(6)(5)=1,2; \\& 5x+4=-10\Rightarrow 5x=-14\Rightarrow x=-\frac(14)(5)=-2,8. \\\end(align)\]

Asta e tot! Avem două rădăcini: $x=1.2$ și $x=-2.8$. Întreaga soluție a luat literalmente două rânduri.

Ok, fără îndoială, hai să ne uităm la ceva mai serios:

\[\stanga| 7-5x \right|=13\]

Din nou, deschideți modulul cu un plus și un minus:

\[\begin(align)& 7-5x=13\Rightarrow -5x=6\Rightarrow x=-\frac(6)(5)=-1,2; \\& 7-5x=-13\Rightarrow -5x=-20\Rightarrow x=4. \\\end(align)\]

Din nou câteva rânduri - și răspunsul este gata! După cum am spus, nu este nimic complicat în module. Trebuie doar să vă amintiți câteva reguli. Prin urmare, mergem mai departe și continuăm cu sarcini cu adevărat mai dificile.

Carcasa din partea dreapta variabila

Acum luați în considerare această ecuație:

\[\stanga| 3x-2 \right|=2x\]

Această ecuație este fundamental diferită de toate precedentele. Cum? Și faptul că expresia $2x$ se află în dreapta semnului egal - și nu putem ști dinainte dacă este pozitivă sau negativă.

Cum să fii în acest caz? În primul rând, trebuie să înțelegem asta odată pentru totdeauna dacă partea dreaptă a ecuației este negativă, atunci ecuația nu va avea rădăcini- știm deja că modulul nu poate fi egal cu un număr negativ.

Și în al doilea rând, dacă partea dreaptă este încă pozitivă (sau egală cu zero), atunci puteți proceda exact în același mod ca înainte: deschideți modulul separat cu semnul plus și separat cu semnul minus.

Astfel, formulăm o regulă pentru funcțiile arbitrare $f\left(x \right)$ și $g\left(x \right)$ :

\[\stanga| f\left(x \right) \right|=g\left(x \right)\Rightarrow \left\( \begin(align)& f\left(x \right)=\pm g\left(x \right) ), \\& g\left(x \right)\ge 0. \\\end(align) \right.\]

În ceea ce privește ecuația noastră, obținem:

\[\stanga| 3x-2 \right|=2x\Rightarrow \left\( \begin(align)& 3x-2=\pm 2x, \\& 2x\ge 0. \\\end(align) \right.\]

Ei bine, ne putem ocupa cumva de cerința $2x\ge 0$. În cele din urmă, putem înlocui prostește rădăcinile pe care le obținem din prima ecuație și putem verifica dacă inegalitatea este valabilă sau nu.

Deci, să rezolvăm ecuația în sine:

\[\begin(align)& 3x-2=2\Rightarrow 3x=4\Rightarrow x=\frac(4)(3); \\& 3x-2=-2\Rightarrow 3x=0\Rightarrow x=0. \\\end(align)\]

Ei bine, care dintre aceste două rădăcini satisface cerința $2x\ge 0$? Da, ambele! Prin urmare, răspunsul va fi două numere: $x=(4)/(3)\;$ și $x=0$. asta e solutia. :)

Bănuiesc că unul dintre elevi a început deja să se plictisească? Ei bine, luați în considerare o ecuație și mai complexă:

\[\stanga| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\]

Deși pare rău, de fapt este aceeași ecuație de forma „modulus equals function”:

\[\stanga| f\stanga(x \dreapta) \dreapta|=g\stanga(x \dreapta)\]

Și se rezolvă în același mod:

\[\stanga| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\Rightarrow \left\( \begin(align)& ( (x)^(3))-3((x)^(2))+x=\pm \left(x-((x)^(3)) \right), \\& x-((x) )^(3))\ge 0. \\\end(align) \right.\]

Ne vom ocupa de inegalitatea mai târziu - este cumva prea vicios (de fapt simplu, dar nu o vom rezolva). Deocamdată, să aruncăm o privire la ecuațiile rezultate. Luați în considerare primul caz - acesta este momentul în care modulul este extins cu un semn plus:

\[((x)^(3))-3((x)^(2))+x=x-((x)^(3))\]

Ei bine, iată că trebuie să adunați totul din stânga, să aduceți altele similare și să vedeți ce se întâmplă. Și iată ce se întâmplă:

\[\begin(align)& ((x)^(3))-3((x)^(2))+x=x-((x)^(3)); \\& 2((x)^(3))-3((x)^(2))=0; \\\end(align)\]

Punând factorul comun $((x)^(2))$ din paranteză, obținem o ecuație foarte simplă:

\[((x)^(2))\left(2x-3 \right)=0\Rightarrow \left[ \begin(align)& ((x)^(2))=0 \\& 2x-3 =0 \\\end(aliniere) \dreapta.\]

\[((x)_(1))=0;\quad ((x)_(2))=\frac(3)(2)=1,5.\]

Aici am folosit proprietate importantă produs, de dragul căruia am factorizat polinomul original: produsul este egal cu zero atunci când cel puțin unul dintre factori este egal cu zero.

Acum, în același mod, ne vom ocupa de a doua ecuație, care se obține prin extinderea modulului cu semnul minus:

\[\begin(align)& ((x)^(3))-3((x)^(2))+x=-\left(x-((x)^(3)) \right); \\& ((x)^(3))-3((x)^(2))+x=-x+((x)^(3)); \\& -3((x)^(2))+2x=0; \\& x\left(-3x+2 \right)=0. \\\end(align)\]

Din nou, același lucru: produsul este zero atunci când cel puțin unul dintre factori este zero. Avem:

\[\left[ \begin(align)& x=0 \\& -3x+2=0 \\\end(align) \right.\]

Ei bine, avem trei rădăcini: $x=0$, $x=1.5$ și $x=(2)/(3)\;$. Ei bine, ce va intra în răspunsul final din acest set? Pentru a face acest lucru, amintiți-vă că avem o constrângere suplimentară de inegalitate:

Cum să ținem cont de această cerință? Să înlocuim doar rădăcinile găsite și să verificăm dacă inegalitatea este valabilă pentru acești $x$ sau nu. Avem:

\[\begin(align)& x=0\Rightarrow x-((x)^(3))=0-0=0\ge 0; \\& x=1,5\Rightarrow x-((x)^(3))=1,5-(((1,5)^(3)) \lt 0; \\& x=\frac(2)(3)\Rightarrow x-((x)^(3))=\frac(2)(3)-\frac(8)(27)=\frac(10) (27)\ge 0; \\\end(align)\]

Astfel, rădăcina $x=1,5$ nu ni se potrivește. Și doar două rădăcini vor merge ca răspuns:

\[((x)_(1))=0;\quad ((x)_(2))=\frac(2)(3).\]

După cum puteți vedea, chiar și în acest caz nu a fost nimic dificil - ecuațiile cu module sunt întotdeauna rezolvate conform algoritmului. Trebuie doar să înțelegeți bine polinoamele și inegalitățile. Prin urmare, trecem la sarcini mai complexe - vor exista deja nu unul, ci două module.

Ecuații cu două module

Până acum, am studiat doar cele mai simple ecuații - a existat un modul și altceva. Am trimis acest „altceva” unei alte părți a inegalității, departe de modul, astfel încât în ​​final totul să fie redus la o ecuație de genul $\left| f\left(x \right) \right|=g\left(x \right)$ sau chiar mai simplu $\left| f\left(x \right) \right|=a$.

Dar Grădiniţă peste - este timpul să luăm în considerare ceva mai serios. Să începem cu ecuații ca aceasta:

\[\stanga| f\left(x \right) \right|=\left| g\stanga(x \dreapta) \dreapta|\]

Aceasta este o ecuație de forma „modulul este egal cu modulul”. Fundamental punct important este absența altor termeni și factori: doar un modul în stânga, încă un modul în dreapta - și nimic mai mult.

S-ar crede acum că astfel de ecuații sunt mai greu de rezolvat decât ceea ce am studiat până acum. Dar nu: aceste ecuații se rezolvă și mai ușor. Iată formula:

\[\stanga| f\left(x \right) \right|=\left| g\left(x \right) \right|\Rightarrow f\left(x \right)=\pm g\left(x \right)\]

Tot! Pur și simplu echivalăm expresiile submodulelor prefixând una dintre ele cu un semn plus sau minus. Și apoi rezolvăm cele două ecuații rezultate - și rădăcinile sunt gata! Fără restricții suplimentare, fără inegalități etc. Totul este foarte simplu.

Să încercăm să rezolvăm această problemă:

\[\stanga| 2x+3 \right|=\left| 2x-7 \dreapta|\]

Primar Watson! Deschiderea modulelor:

\[\stanga| 2x+3 \right|=\left| 2x-7 \right|\Rightarrow 2x+3=\pm \left(2x-7 \right)\]

Să luăm în considerare fiecare caz separat:

\[\begin(align)& 2x+3=2x-7\Rightarrow 3=-7\Rightarrow \emptyset ; \\& 2x+3=-\left(2x-7 \right)\Rightarrow 2x+3=-2x+7. \\\end(align)\]

Prima ecuație nu are rădăcini. Pentru că când este $3=-7$? Pentru ce valori de $x$? „Ce dracu este $x$? Esti drogat? Nu există $x$ deloc”, spuneți. Și vei avea dreptate. Am obținut o egalitate care nu depinde de variabila $x$ și, în același timp, egalitatea în sine este incorectă. De aceea nu există rădăcini.

Cu a doua ecuație, totul este puțin mai interesant, dar și foarte, foarte simplu:

După cum puteți vedea, totul a fost decis literalmente în câteva rânduri - nu ne așteptam la nimic altceva de la o ecuație liniară. :)

Ca urmare, răspunsul final este: $x=1$.

Ei bine, cum? Dificil? Desigur că nu. Să încercăm altceva:

\[\stanga| x-1 \right|=\left| ((x)^(2))-3x+2 \dreapta|\]

Din nou avem o ecuație ca $\left| f\left(x \right) \right|=\left| g\left(x \right) \right|$. Prin urmare, îl rescriem imediat, dezvăluind semnul modulului:

\[((x)^(2))-3x+2=\pm \left(x-1 \right)\]

Poate că cineva va întreba acum: „Hei, ce fel de prostii? De ce este plus-minus pe partea dreaptă și nu pe partea stângă? Calmează-te, o să explic totul. Într-adevăr, într-un sens bun, ar fi trebuit să ne rescriem ecuația după cum urmează:

Apoi trebuie să deschideți parantezele, să mutați toți termenii într-o direcție din semnul egal (deoarece ecuația, evident, va fi pătrată în ambele cazuri) și apoi să găsiți rădăcinile. Dar trebuie să recunoașteți: când „plus-minus” este în fața a trei termeni (mai ales când unul dintre acești termeni este o expresie pătrată), pare cumva mai complicată decât situația când „plus-minus” este doar în fața a doi. termeni.

Dar nimic nu ne împiedică să rescriem ecuația originală după cum urmează:

\[\stanga| x-1 \right|=\left| ((x)^(2))-3x+2 \right|\Rightarrow \left| ((x)^(2))-3x+2 \right|=\left| x-1 \dreapta|\]

Ce s-a întâmplat? Da, nimic special: doar am schimbat partea stângă și cea dreaptă. Un fleac, care până la urmă ne va simplifica puțin viața. :)

În general, rezolvăm această ecuație, luând în considerare opțiunile cu plus și minus:

\[\begin(align)& ((x)^(2))-3x+2=x-1\Rightarrow ((x)^(2))-4x+3=0; \\& ((x)^(2))-3x+2=-\left(x-1 \right)\Rightarrow ((x)^(2))-2x+1=0. \\\end(align)\]

Prima ecuație are rădăcini $x=3$ și $x=1$. Al doilea este, în general, un pătrat exact:

\[((x)^(2))-2x+1=((\left(x-1 \right))^(2))\]

Prin urmare, are o singură rădăcină: $x=1$. Dar am primit deja această rădăcină mai devreme. Astfel, doar două numere vor intra în răspunsul final:

\[((x)_(1))=3;\quad ((x)_(2))=1.\]

Misiune indeplinita! Poți să-l iei de pe raft și să mănânci o plăcintă. Sunt 2, media ta. :)

Notă importantă. Avand aceleasi radacini opțiuni diferite extinderea modulului înseamnă că polinoamele originale sunt descompuse în factori, iar printre acești factori va fi neapărat unul comun. Într-adevăr:

\[\begin(align)&\left| x-1 \right|=\left| ((x)^(2))-3x+2 \right|; \\&\stânga| x-1 \right|=\left| \left(x-1 \right)\left(x-2 \right) \right|. \\\end(align)\]

Una dintre proprietățile modulului: $\left| a\cdot b \right|=\left| a \right|\cdot \left| b \right|$ (adică modulul produsului este egal cu produsul modulelor), deci ecuația originală poate fi rescrisă ca

\[\stanga| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \dreapta|\]

După cum puteți vedea, avem într-adevăr un factor comun. Acum, dacă colectați toate modulele pe o singură parte, atunci puteți scoate acest multiplicator din paranteză:

\[\begin(align)&\left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \dreapta|; \\&\stânga| x-1 \right|-\left| x-1 \right|\cdot \left| x-2 \right|=0; \\&\stânga| x-1 \right|\cdot \left(1-\left| x-2 \right| \right)=0. \\\end(align)\]

Ei bine, acum ne amintim că produsul este egal cu zero atunci când cel puțin unul dintre factori este egal cu zero:

\[\left[ \begin(align)& \left| x-1 \right|=0, \\& \left| x-2 \right|=1. \\\end(aliniere) \dreapta.\]

Astfel, ecuația originală cu două module a fost redusă la cele mai simple două ecuații despre care am vorbit chiar la începutul lecției. Astfel de ecuații pot fi rezolvate în doar câteva rânduri. :)

Această remarcă poate părea inutil de complicată și inaplicabilă în practică. Cu toate acestea, în realitate, puteți întâlni sarcini mult mai complexe decât cele pe care le analizăm astăzi. În ele, modulele pot fi combinate cu polinoame, rădăcini aritmetice, logaritmi etc. Și în astfel de situații, capacitatea de a scădea gradul general al ecuației prin scoaterea a ceva din paranteză poate fi foarte, foarte utilă. :)

Acum aș vrea să analizez o altă ecuație, care la prima vedere poate părea nebunească. Mulți studenți se „lipesc” de el - chiar și cei care cred că au o bună înțelegere a modulelor.

Cu toate acestea, această ecuație este chiar mai ușor de rezolvat decât ceea ce am considerat mai devreme. Și dacă înțelegeți de ce, veți obține un alt truc pentru rezolvarea rapidă a ecuațiilor cu module.

Deci ecuația este:

\[\stanga| x-((x)^(3)) \dreapta|+\stânga| ((x)^(2))+x-2 \right|=0\]

Nu, aceasta nu este o greșeală de tipar: este un plus între module. Și trebuie să aflăm pentru care $x$ suma a două module este egală cu zero. :)

Care este problema? Și problema este că fiecare modul este un număr pozitiv sau, în cazuri extreme, zero. Ce se întâmplă când adunăm două numere pozitive? Evident, din nou un număr pozitiv:

\[\begin(align)& 5+7=12 \gt 0; \\& 0,004+0,0001=0,0041 \gt 0; \\& 5+0=5 \gt 0. \\\end(align)\]

Ultima linie vă poate oferi o idee: singurul caz în care suma modulelor este zero este dacă fiecare modul este egal cu zero:

\[\stanga| x-((x)^(3)) \dreapta|+\stânga| ((x)^(2))+x-2 \right|=0\Rightarrow \left\( \begin(align)& \left| x-((x)^(3)) \right|=0, \\& \left|((x)^(2))+x-2 \right|=0. \\\end(align) \right.\]

Când este modulul egal cu zero? Doar într-un caz - când expresia submodulului este egală cu zero:

\[((x)^(2))+x-2=0\Rightarrow \left(x+2 \right)\left(x-1 \right)=0\Rightarrow \left[ \begin(align)& x=-2 \\& x=1 \\\end(align) \right.\]

Astfel, avem trei puncte la care primul modul este setat la zero: 0, 1 și −1; precum și două puncte în care al doilea modul este pus la zero: −2 și 1. Totuși, avem nevoie ca ambele module să fie puse la zero în același timp, așa că dintre numerele găsite, trebuie să le alegem pe cele care sunt incluse în ambele mulțimi. Evident, există un singur astfel de număr: $x=1$ - acesta va fi răspunsul final.

metoda de divizare

Ei bine, am acoperit deja o grămadă de sarcini și am învățat o mulțime de trucuri. Crezi că asta este? Dar nu! Acum vom lua în considerare tehnica finală - și, în același timp, cea mai importantă. Vom vorbi despre împărțirea ecuațiilor cu un modul. Ce se va discuta? Să ne întoarcem puțin și să luăm în considerare o ecuație simplă. De exemplu, aceasta:

\[\stanga| 3x-5\right|=5-3x\]

În principiu, știm deja cum să rezolvăm o astfel de ecuație, deoarece este un standard $\left| f\left(x \right) \right|=g\left(x \right)$. Dar să încercăm să privim această ecuație dintr-un unghi ușor diferit. Mai precis, luați în considerare expresia de sub semnul modulului. Permiteți-mi să vă reamintesc că modulul oricărui număr poate fi egal cu numărul în sine sau poate fi opus acestui număr:

\[\stanga| a \right|=\left\( \begin(align)& a,\quad a\ge 0, \\& -a,\quad a \lt 0. \\\end(align) \right.\]

De fapt, această ambiguitate este întreaga problemă: deoarece numărul de sub modul se modifică (depinde de variabilă), nu ne este clar dacă este pozitiv sau negativ.

Dar ce se întâmplă dacă inițial solicităm ca acest număr să fie pozitiv? De exemplu, să cerem că $3x-5 \gt 0$ - în acest caz, suntem garantați să obținem un număr pozitiv sub semnul modulului și putem scăpa complet de acest modul:

Astfel, ecuația noastră se va transforma într-una liniară, care se rezolvă ușor:

Adevărat, toate aceste considerații au sens numai în condiția $3x-5 \gt 0$ - noi înșine am introdus această cerință pentru a dezvălui fără ambiguitate modulul. Deci, să înlocuim $x=\frac(5)(3)$ găsit în această condiție și să verificăm:

Se pare că pentru valoarea specificată de $x$, cerința noastră nu este îndeplinită, deoarece expresia sa dovedit a fi egală cu zero și trebuie să fie strict mai mare decât zero. Trist. :(

Dar este în regulă! La urma urmei, există o altă opțiune $3x-5 \lt 0$. Mai mult: există și cazul $3x-5=0$ - trebuie luat în considerare și acest lucru, altfel soluția va fi incompletă. Deci, luați în considerare cazul $3x-5 \lt 0$:

Este evident că modulul se va deschide cu semnul minus. Dar atunci apare o situație ciudată: aceeași expresie va ieși atât în ​​stânga, cât și în dreapta în ecuația originală:

Mă întreb pentru ce astfel de $x$ va fi expresia $5-3x$ egală cu expresia $5-3x$? Din astfel de ecuații, chiar și Căpitanul s-ar îneca evident cu salivă, dar știm că această ecuație este o identitate, adică. este valabil pentru orice valoare a variabilei!

Și asta înseamnă că orice $x$ ne va potrivi. Cu toate acestea, avem o limitare:

Cu alte cuvinte, răspunsul nu va fi un singur număr, ci un întreg interval:

În cele din urmă, mai rămâne un caz de luat în considerare: $3x-5=0$. Totul este simplu aici: va fi zero sub modul, iar modulul lui zero este, de asemenea, egal cu zero (acest lucru decurge direct din definiție):

Dar apoi ecuația originală $\left| 3x-5 \right|=5-3x$ va fi rescris astfel:

Am obținut deja această rădăcină mai sus când am luat în considerare cazul $3x-5 \gt 0$. Mai mult, această rădăcină este o soluție a ecuației $3x-5=0$ - aceasta este restricția pe care noi înșine am introdus-o pentru a anula modulul. :)

Astfel, pe lângă interval, vom fi mulțumiți și de numărul care se află la sfârșitul acestui interval:

Combinarea rădăcinilor în ecuații cu modul

Răspuns final total: $x\in \left(-\infty ;\frac(5)(3) \right]$. Nu este foarte obișnuit să vezi o astfel de prostie în răspunsul la o ecuație destul de simplă (în esență liniară) cu modul Ei bine, obișnuiește-te cu asta: complexitatea modulului constă în faptul că răspunsurile în astfel de ecuații pot fi complet imprevizibile.

Mult mai important este altceva: tocmai am demontat un algoritm universal pentru rezolvarea unei ecuații cu un modul! Și acest algoritm constă din următorii pași:

1. Echivalați fiecare modul din ecuație cu zero. Să obținem câteva ecuații;
2. Rezolvați toate aceste ecuații și marcați rădăcinile pe dreapta numerică. Drept urmare, linia dreaptă va fi împărțită în mai multe intervale, pe fiecare dintre acestea toate modulele sunt extinse în mod unic;
3. Rezolvați ecuația inițială pentru fiecare interval și combinați răspunsurile.

Asta e tot! Rămâne o singură întrebare: ce să faci cu rădăcinile în sine, obținute la primul pas? Să presupunem că avem două rădăcini: $x=1$ și $x=5$. Ei vor sparge linia numerică în 3 bucăți:

Împărțirea unei linii numerice în intervale folosind puncte

Deci care sunt intervalele? Este clar că sunt trei dintre ele:

1. Cel mai din stânga: $x \lt 1$ - unitatea în sine nu este inclusă în interval;
2. Central: $1\le x \lt 5$ - aici unul este inclus în interval, dar cinci nu este inclus;
3. Cea din dreapta: $x\ge 5$ — cele cinci sunt incluse doar aici!

Cred că ai înțeles deja modelul. Fiecare interval include capătul din stânga și nu include capătul din dreapta.

La prima vedere, o astfel de înregistrare poate părea incomodă, ilogică și, în general, un fel de nebunie. Dar credeți-mă: după puțină practică, veți descoperi că aceasta este cea mai fiabilă abordare și, în același timp, nu interferează cu dezvăluirea fără ambiguitate a modulelor. Este mai bine să folosiți o astfel de schemă decât să vă gândiți de fiecare dată: dați capătul din stânga/dreapta intervalului curent sau „aruncați-l” celui următor.

Acest calculator de matematică online vă va ajuta rezolvarea unei ecuații sau inegalități cu module. Program pentru rezolvarea de ecuații și inegalități cu module nu numai că oferă răspunsul problemei, ci conduce solutie detaliata cu explicatii, adică afișează procesul de obținere a rezultatului.

Acest program poate fi util elevilor de liceu scoli de invatamant generalîn pregătire pentru munca de controlși examene, la testarea cunoștințelor înainte de examen, părinții pentru a controla rezolvarea multor probleme de matematică și algebră. Sau poate este prea scump pentru tine să angajezi un tutor sau să cumperi noi manuale? Sau vrei doar să o faci cât mai curând posibil? teme pentru acasă matematica sau algebra? În acest caz, puteți utiliza și programele noastre cu o soluție detaliată.

În acest fel, vă puteți conduce propriul antrenament și/sau vă puteți antrena frati mai mici sau surori, în timp ce nivelul de educație în domeniul sarcinilor în curs de rezolvare crește.

|x| sau abs(x) - modulul x

Introduceți ecuația sau inegalitatea cu module

Rezolvați o ecuație sau o inegalitate

S-a constatat că unele scripturi necesare pentru a rezolva această sarcină nu au fost încărcate și este posibil ca programul să nu funcționeze.
Este posibil să aveți AdBlock activat.
În acest caz, dezactivați-l și reîmprospătați pagina.

Aveți JavaScript dezactivat în browser.
JavaScript trebuie să fie activat pentru ca soluția să apară.
Iată instrucțiuni despre cum să activați JavaScript în browserul dvs.

pentru că Sunt o mulțime de oameni care doresc să rezolve problema, cererea ta este pusă în coadă.
După câteva secunde, soluția va apărea mai jos.
Asteapta te rog sec...

daca tu observat o eroare în soluție, apoi puteți scrie despre asta în Formularul de feedback .
Nu uita indicați ce sarcină tu decizi ce intra in campuri.

Jocurile, puzzle-urile, emulatorii noștri:

Un pic de teorie.

Ecuații și inegalități cu module

În cursul de algebră școlară de bază, puteți întâlni cele mai simple ecuații și inegalități cu module. Pentru a le rezolva, puteți aplica o metodă geometrică bazată pe faptul că \(|x-a| \) este distanța pe dreapta numerică dintre punctele x și a: \(|x-a| = \rho (x;\; a) ) \). De exemplu, pentru a rezolva ecuația \(|x-3|=2 \), trebuie să găsiți puncte pe dreapta numerică care sunt la o distanță de 2 de punctul 3. Există două astfel de puncte: \(x_1=1 \) și \(x_2=5 \) .

Rezolvarea inegalității \(|2x+7|

Dar principala modalitate de a rezolva ecuații și inegalități cu module este legată de așa-numita „extindere a modulelor prin definiție”:
dacă \(a \geq 0 \), atunci \(|a|=a \);
dacă \(a De regulă, o ecuație (inegalitate) cu module se reduce la un set de ecuații (inegalități) care nu conțin semnul modulului.

Pe lângă definiția de mai sus, se folosesc următoarele afirmații:
1) Dacă \(c > 0 \), atunci ecuația \(|f(x)|=c \) este echivalentă cu mulțimea de ecuații: \(\left[\begin(array)(l) f(x )=c \\ f(x)=-c \end(matrice)\dreapta.\)
2) Dacă \(c > 0 \), atunci inegalitatea \(|f(x)| 3) Dacă \(c \geq 0 \), atunci inegalitatea \(|f(x)| > c \) este echivalent cu mulțimea de inegalități : \(\left[\begin(array)(l) f(x) c \end(array)\right. \)
4) Dacă ambele părți ale inegalității \(f(x) EXEMPLU 1. Rezolvați ecuația \(x^2 +2|x-1| -6 = 0 \).

Dacă \(x-1 \geq 0 \), atunci \(|x-1| = x-1 \) și ecuația dată devine
\(x^2 +2(x-1) -6 = 0 \Rightarrow x^2 +2x -8 = 0 \).
Dacă \(x-1 \(x^2 -2(x-1) -6 = 0 \Rightarrow x^2 -2x -4 = 0 \).
Astfel, ecuația dată trebuie luată în considerare separat în fiecare dintre cele două cazuri indicate.
1) Fie \(x-1 \geq 0 \), i.e. \(x \geq 1 \). Din ecuația \(x^2 +2x -8 = 0 \) găsim \(x_1=2, \; x_2=-4\). Condiția \(x \geq 1 \) este îndeplinită numai de valoarea \(x_1=2\).
2) Fie \(x-1 Răspuns: \(2; \;\; 1-\sqrt(5) \)

EXEMPLU 2. Rezolvați ecuația \(|x^2-6x+7| = \frac(5x-9)(3) \).

Prima cale(extinderea modulului prin definiție).
Argumentând ca în exemplul 1, concluzionăm că ecuația dată trebuie considerată separat în două condiții: \(x^2-6x+7 \geq 0 \) sau \(x^2-6x+7

1) Dacă \(x^2-6x+7 \geq 0 \), atunci \(|x^2-6x+7| = x^2-6x+7 \) și ecuația dată devine \(x^2 -6x+7 = \frac(5x-9)(3) \Rightarrow 3x^2-23x+30=0 \). Rezolvarea ecuație pătratică, obținem: \(x_1=6, \; x_2=\frac(5)(3) \).
Să aflăm dacă valoarea \(x_1=6 \) satisface condiția \(x^2-6x+7 \geq 0 \). Pentru a face acest lucru, înlocuim valoarea indicată în inegalitatea pătratică. Se obține: \(6^2-6 \cdot 6+7 \geq 0 \), adică. \(7 \geq 0 \) este inegalitatea corectă. Prin urmare, \(x_1=6 \) este rădăcina ecuației date.
Să aflăm dacă valoarea \(x_2=\frac(5)(3) \) satisface condiția \(x^2-6x+7 \geq 0 \). Pentru a face acest lucru, înlocuim valoarea indicată în inegalitatea pătratică. Se obține: \(\left(\frac(5)(3) \right)^2 -\frac(5)(3) \cdot 6 + 7 \geq 0 \), adică. \(\frac(25)(9) -3 \geq 0 \) este o inegalitate nevalidă. Deci \(x_2=\frac(5)(3) \) nu este o rădăcină a ecuației date.

2) Dacă \(x^2-6x+7 Valoarea \(x_3=3\) satisface condiția \(x^2-6x+7 Valoarea \(x_4=\frac(4)(3) \) nu nu satisface condiția \ (x^2-6x+7 Deci, ecuația dată are două rădăcini: \(x=6, \; x=3 \).

A doua cale. Având în vedere o ecuație \(|f(x)| = h(x) \), atunci pentru \(h(x) \(\left[\begin(array)(l) x^2-6x+7 = \frac (5x-9)(3) \\ x^2-6x+7 = -\frac(5x-9)(3) \end(array)\right. \)
Ambele ecuații sunt rezolvate mai sus (cu prima metodă de rezolvare a ecuației date), rădăcinile lor sunt după cum urmează: \(6,\; \frac(5)(3),\; 3,\; \frac(4) )(3) \). Condiția \(\frac(5x-9)(3) \geq 0 \) a acestora patru valori satisface doar două: 6 și 3. Prin urmare, ecuația dată are două rădăcini: \(x=6, \; x=3 \).

A treia cale(grafic).
1) Să reprezentăm grafic funcția \(y = |x^2-6x+7| \). Mai întâi construim o parabolă \(y = x^2-6x+7\). Avem \(x^2-6x+7 = (x-3)^2-2 \). Graficul funcției \(y = (x-3)^2-2 \) poate fi obținut din graficul funcției \(y = x^2 \) deplasând-o cu 3 unități de scară la dreapta (pe axa x) și 2 unități de scară în jos (de-a lungul axei y). Linia dreaptă x=3 este axa parabolei care ne interesează. La fel de puncte de control pentru o reprezentare mai precisă, este convenabil să luați punctul (3; -2) - vârful parabolei, punctul (0; 7) și punctul (6; 7) simetric față de acesta față de axa parabolei. parabolă.
Pentru a construi acum graficul funcției \(y = |x^2-6x+7| \), trebuie să lăsați neschimbate acele părți ale parabolei construite care nu se află sub axa x și oglindiți partea din parabolă. parabola care se află sub axa x în jurul axei x.
2) Să construim un grafic funcție liniară\(y = \frac(5x-9)(3) \). Este convenabil să luați punctele (0; –3) și (3; 2) ca puncte de control.

Este esențial ca punctul x = 1,8 al intersecției dreptei cu axa absciselor să fie situat la dreapta punctului de intersecție din stânga al parabolei cu axa absciselor - acesta este punctul \(x=3-\sqrt (2) \) (deoarece \(3-\sqrt(2 ) 3) Judecând după desen, graficele se intersectează în două puncte - A (3; 2) și B (6; 7). Înlocuind abscisele acestor puncte x \u003d 3 și x \u003d 6 în ecuația dată, ne asigurăm că ambele alte valori oferă egalitatea numerică corectă. Deci, ipoteza noastră a fost confirmată - ecuația are două rădăcini: x \u003d 3 și x \u003d 6. Răspuns: 3; 6.

cometariu. Mod grafic cu toată eleganța sa, nu este foarte de încredere. În exemplul luat în considerare, a funcționat doar pentru că rădăcinile ecuației sunt numere întregi.

EXEMPLU 3. Rezolvați ecuația \(|2x-4|+|x+3| = 8 \)

Prima cale
Expresia 2x–4 devine 0 în punctul x = 2, iar expresia x + 3 în punctul x = –3. Aceste două puncte împart linia numerică în trei intervale: \(x

Luați în considerare primul interval: \((-\infty; \; -3) \).
Dacă x Luați în considerare al doilea interval: \([-3; \; 2) \).
Dacă \(-3 \leq x Luați în considerare al treilea interval: \(. Acum extindeți modulul interior pentru x>2.5 . Obțineți o ecuație cu un modul
|2x-5-1|=x+3;
|2x-6|=x+3.
Când extindem modulul, obținem următoarele ecuatii lineare
-2x+6=x+3 sau 2x-6=x+3;
2x+x=6-3 sau 2x-x=3+6;
3x=3; x=1 sau x=9.
Prima valoare x=1 nu satisface conditia x>2,5. Deci pe acest interval avem o rădăcină a ecuației cu modulul x=9, și sunt doar două dintre ele (x=1/3).Prin substituție, puteți verifica corectitudinea calculelor efectuate.
Raspuns: x=1/3; x=9.

Exemplul 4 Aflați soluții ale modulului dublu ||3x-1|-5|=2x-3.
Rezolvare: Extindeți modulul interior al ecuației
|3x-1|=0 <=>x=1/3.
Punctul x=2,5 împarte axa numerică în două intervale, iar ecuația dată în două cazuri. Notăm condiția pentru soluție, pe baza formei ecuației cu partea dreapta
2x-3>=0 -> x>=3/2=1,5.
Rezultă că ne interesează valorile >=1,5. În acest fel ecuație modulară uită-te la două intervale
,
|-(3x-1)-5|=2x-3;
|-3x-4|=2x-3.
Modulul rezultat, atunci când este extins, este împărțit în 2 ecuații
-3x-4=2x-3 sau 3x+4=2x-3;
2x+3x=-4+3 sau 3x-2x=-3-4;
5x=-1; x=-1/5 sau x=-7.
Ambele valori nu se încadrează în interval, adică nu sunt soluții ale ecuației cu module. Apoi, extindeți modulul pentru x>2,5. Obținem următoarea ecuație
|3x-1-5|=2x-3;
|3x-6|=2x-3.
Extinderea modulului obținem 2 ecuații liniare
3x-6=2x-3 sau –(3x-6)=2x-3;
3x-2x=-3+6 sau 2x+3x=6+3;
x=3 sau 5x=9; x=9/5=1,8.
A doua valoare găsită nu îndeplinește condiția x>2,5, o respingem.
În cele din urmă avem o rădăcină a ecuației cu module x=3 .
Efectuăm o verificare
||3*3-1|-5|=2*3-3 3=3 .
Rădăcina ecuației cu modulul calculat corect.
Raspuns: x=1/3; x=9.

MBOU gimnaziu №17 Ivanov

« Ecuații de modul»
Dezvoltare metodică

Compilat

profesor de matematica

Lebedeva N.V.

20010

Notă explicativă

Capitolul 1 Introducere

Secțiunea 2. Caracteristici principale Secțiunea 3. Interpretarea geometrică a conceptului de modul al unui număr Secțiunea 4. Graficul funcției y = |x| Secțiunea 5 Convenții

capitolul 2

Secțiunea 1. Ecuații de forma |F(х)| = m (protozoare) Secțiunea 2. Ecuații de forma F(|х|) = m Secțiunea 3. Ecuații de forma |F(х)| = G(x) Secțiunea 4. Ecuații de forma |F(х)| = ± F(x) (frumos) Secțiunea 5. Ecuații de forma |F(х)| = |G(x)| Secțiunea 6. Exemple de rezolvare a ecuațiilor nestandard Secțiunea 7. Ecuații de forma |F(х)| + |G(x)| = 0 Secțiunea 8. Ecuații de forma |а 1 x ± в 1 | ± |a 2 x ± în 2 | ± …|a n x ± în n | = m Secțiunea 9. Ecuații care conțin module multiple

Capitolul 3. Exemple de rezolvare a diverselor ecuații cu un modul.

Secțiunea 1. Ecuații trigonometrice Secțiunea 2. Ecuații exponențiale Secțiunea 3 Ecuații logaritmice Secțiunea 4. Ecuații iraționale Secțiunea 5. Atribuții complexitate crescută Răspunsuri la exerciții Bibliografie

Notă explicativă.

Conceptul de valoare absolută (modul) a unui număr real este una dintre caracteristicile sale esențiale. Acest concept este utilizat pe scară largă în diferite ramuri ale științelor fizice, matematice și tehnice. În practica predării unui curs de matematică în liceuîn conformitate cu Programul Ministerului Apărării al Federației Ruse, conceptul de „valoarea absolută a unui număr” apare în mod repetat: în clasa a VI-a, este introdusă o definiție a modulului, sa sens geometric; în clasa a VIII-a se formează conceptul de eroare absolută, se consideră soluția celor mai simple ecuații și inegalități care conțin modulul, proprietățile aritmeticii rădăcină pătrată; în clasa a XI-a conceptul se regăsește la secțiunea „Rădăcină ngradul”. Experiența de predare arată că elevii întâmpină adesea dificultăți în rezolvarea sarcinilor care necesită cunoștințe acest material, și adesea omis fără a începe execuția. În texte sarcini de examinare pentru cursul claselor a IX-a și a XI-a sunt incluse și sarcini similare. În plus, cerințele pe care universitățile le impun absolvenților de școală diferă și anume mai mult nivel inalt decât cerințele programului școlar. Pentru viata in societate modernă foarte importantă este formarea unui stil matematic de gândire, manifestat în anumite aptitudini mentale. În procesul de rezolvare a problemelor cu module, este necesară abilitatea de a aplica tehnici precum generalizarea și concretizarea, analiza, clasificarea și sistematizarea, analogia. Rezolvarea unor astfel de sarcini vă permite să verificați cunoștințele principalelor secțiuni curs şcolar, nivel gandire logica, abilități inițiale de cercetare. acest lucru este dedicat uneia dintre secțiuni - soluția ecuațiilor care conțin modulul. Este format din trei capitole. Primul capitol prezintă conceptele de bază și cele mai importante calcule teoretice. Al doilea capitol propune nouă tipuri de bază de ecuații care conțin modulul, ia în considerare metode de rezolvare a acestora și analizează exemple diferite niveluri dificultăți. Al treilea capitol oferă ecuații mai complexe și non-standard (trigonometrice, exponențiale, logaritmice și iraționale). Pentru fiecare tip de ecuații există exerciții pentru decizie independentă(răspunsurile și instrucțiunile sunt atașate). Scopul principal al acestei lucrări este de a oferi asistență metodologică profesorilor în pregătirea lecțiilor și în organizarea cursurilor opționale. Materialul poate fi folosit și ca ghid de studiu pentru elevii de liceu. Sarcinile oferite în lucrare sunt interesante și nu întotdeauna ușor de rezolvat, ceea ce vă permite să le faceți motivația de învățare studenții mai conștienți, își testează abilitățile, îmbunătățesc nivelul de pregătire al absolvenților de școală pentru a intra în universități. O selecție diferențiată a exercițiilor propuse presupune o trecere de la nivelul reproductiv de asimilare a materialului la cel creativ, precum și posibilitatea de a preda cum să-și aplice cunoștințele în rezolvarea unor probleme nestandardizate.

Capitolul 1 Introducere.

Secțiunea 1. Determinarea valorii absolute .

Definiție : Valoarea absolută (modulul) unui număr real A se numește număr nenegativ: A sau -A. Desemnare: │ A │ Intrarea sună după cum urmează: „modulul numărului a” sau „valoarea absolută a numărului a”

│ a dacă a > 0

│a│ = │ 0 dacă a = 0 (1)

│ - a, dacă a
Exemple: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Extindeți modulul de expresie:

a) │x - 8│ dacă x > 12 b) │2x + 3│ dacă x ≤ -2 │x - 8│= x - 8 │ 2x + 3│= - 2x - 3

Secțiunea 2. Proprietăți de bază.

Luați în considerare proprietățile de bază ale valorii absolute. Proprietatea #1: Numerele opuse au module egale, adică │а│=│-а│ Să arătăm corectitudinea egalității. Să notăm definiția numărului - A : │- a│= (2) Să comparăm seturile (1) și (2). Este evident că definiţiile valori absolute numere Ași - A Meci. Prin urmare, │а│=│-а│
Când luăm în considerare următoarele proprietăți, ne limităm la formularea lor, deoarece demonstrația lor este dată în Proprietatea #2: Valoarea absolută a sumei unui număr finit de numere reale nu depășește suma valorilor absolute ale termenilor: Proprietatea #3: Valoarea absolută a diferenței dintre două numere reale nu depășește suma valorilor lor absolute: │а - в│ ≤│а│+│в│ Proprietatea #4: Valoarea absolută a produsului unui număr finit de numere reale este egală cu produsul valorilor absolute ale factorilor: │а · в│=│а│·│в│ Proprietatea #5: Valoarea absolută a câtului numerelor reale este egală cu câtul valorilor lor absolute:

Secțiunea 3. Interpretarea geometrică a conceptului de modul al unui număr.

Fiecare număr real poate fi asociat cu un punct de pe dreapta numerică, care va fi o reprezentare geometrică a acestui număr real. Fiecare punct de pe dreapta numerică corespunde distanței sale de la origine, adică. lungimea segmentului de la origine la punctul dat. Această distanță este întotdeauna considerată o valoare nenegativă. Prin urmare, lungimea segmentului corespunzător va fi interpretarea geometrică a valorii absolute a numărului real dat

Ilustrația geometrică prezentată confirmă în mod clar proprietatea nr. 1, adică. modulele numerelor opuse sunt egale. De aici, validitatea egalității este ușor de înțeles: │x - a│= │a - x│. De asemenea, devine mai evident să se rezolve ecuația │х│= m, unde m ≥ 0, și anume x 1,2 = ± m. Exemple: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2; patru

Secțiunea 4. Graficul funcției y \u003d │х│

Domeniul acestei funcții este reprezentat de toate numerele reale.

Secțiunea 5. Simboluri.

În viitor, atunci când se vor lua în considerare exemple de rezolvare a ecuațiilor, se vor folosi următoarele. conventii: ( - semn de sistem [ - semn de set La rezolvarea unui sistem de ecuații (inegalități) se găsește intersecția soluțiilor ecuațiilor (inegalităților) incluse în sistem. La rezolvarea unei mulțimi de ecuații (inegalități) se găsește o uniune de soluții a ecuațiilor (inegalităților) incluse în mulțime.

capitolul 2

În acest capitol, vom analiza modalități algebrice de a rezolva ecuații care conțin unul sau mai multe module.

Secțiunea 1. Ecuații de forma │F (х) │= m

O ecuație de acest tip se numește cea mai simplă. Are o soluție dacă și numai dacă m ≥ 0. Prin definiția modulului, ecuația inițială este echivalentă cu combinația a două ecuații: │ F(x)│=m
Exemple:
№1. Rezolvați ecuația: │7x - 2│= 9


Raspuns: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 + 3x = 0 x 1 = -1; x 2 \u003d -2 x (x + 3) \u003d 0 x 1 \u003d 0; x 2 = -3 Răspuns: suma rădăcinilor este - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 - 5x 2 = 0 x 4 - 5x 2 + 4 = 0 x 2 (x 2 - 5) = 0 indică x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – ambele valori satisfac condiția m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Răspuns: numărul de rădăcini ale ecuației 7. Exerciții:
№1. Rezolvați ecuația și indicați suma rădăcinilor: │x - 5│= 3 №2 . Rezolvați ecuația și indicați rădăcina mai mică: │x 2 + x │ \u003d 0 №3 . Rezolvați ecuația și indicați rădăcina mai mare: │x 2 - 5x + 4 │ \u003d 4 №4 .Rezolvați ecuația și indicați întreaga rădăcină: │2x 2 - 7x + 6│ \u003d 1 №5 .Rezolvați ecuația și indicați numărul de rădăcini: │x 4 - 13x 2 + 50 │ = 14

Secțiunea 2. Ecuații de forma F(│х│) = m

Argumentul funcției din partea stângă se află sub semnul modulo, în timp ce partea dreaptă este independentă de variabilă. Să luăm în considerare două moduri de rezolvare a ecuațiilor de acest tip. 1 cale: Prin definiția valorii absolute, ecuația inițială este echivalentă cu totalitatea a două sisteme. În fiecare dintre acestea se impune o condiție expresiei submodulului. F(│х│) =m
Deoarece funcția F(│х│) este pară pe întregul domeniu de definiție, rădăcinile ecuațiilor F(х) = m și F(-х) = m sunt perechi de numere opuse. Prin urmare, este suficientă rezolvarea unuia dintre sisteme (când se consideră exemplele în acest fel, se va da soluția unui sistem). 2 moduri: Aplicarea metodei introducerii unei noi variabile. În acest caz, se introduce denumirea │х│= a, unde a ≥ 0. Aceasta metoda mai puțin voluminos în design.
Exemple: №1 . Rezolvați ecuația: 3x 2 - 4│x│ = - 1 Să folosim introducerea unei noi variabile. Notăm │x│= a, unde a ≥ 0. Obținem ecuația 3a 2 - 4a + 1 = 0 D = 16 - 12 = 4 a 1 = 1 a 2 = 1 / 3 Revenim la variabila inițială: │x │ = 1 și │х│= 1/3. Fiecare ecuație are două rădăcini. Raspuns: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Rezolvați ecuația: 5x 2 + 3│x│- 1 \u003d 1 / 2 │x│ + 3x 2
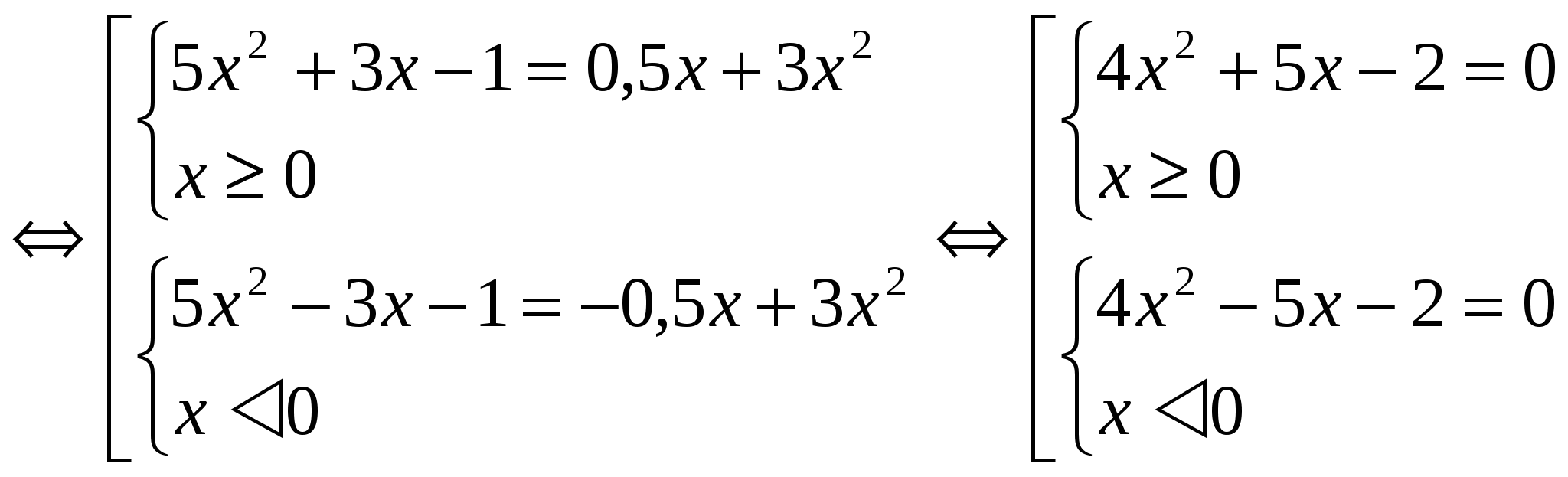Să găsim soluția primului sistem de mulțimi: 4x 2 + 5x - 2 \u003d 0 D \u003d 57 x 1 \u003d -5 + √57 / 8 x 2 \u003d -5-√57 / 8 Rețineți că x 2 face nu satisface condiția x ≥ 0. Prin soluție al doilea sistem va fi numărul opus x 1 . Raspuns: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Rezolvați ecuația: x 4 - │х│= 0 Notăm │х│= a, unde a ≥ 0. Obținem ecuația a 4 - a \u003d 0 a (a 3 - 1) \u003d 0 a 1 \u003d 0 a 2 \u003d 1 Revenim la variabila originală: │х│=0 și │х│= 1 x = 0; ± 1 Raspuns: x 1 = 0; X 2 = 1; X 3 = - 1.
Exerciții: №6. Rezolvați ecuația: 2│х│ - 4,5 = 5 - 3/8 │х│ №7 . Rezolvați ecuația, în răspuns indicați numărul de rădăcini: 3x 2 - 7│x│ + 2 = 0 №8 . Rezolvați ecuația, în răspuns indicați soluțiile întregi: x 4 + │х│ - 2 = 0

Secțiunea 3. Ecuații de forma │F(х)│ = G(х)

Partea dreaptă a unei ecuații de acest tip depinde de o variabilă și, prin urmare, are o soluție dacă și numai dacă partea dreaptă este o funcție G(x) ≥ 0. Ecuația inițială poate fi rezolvată în două moduri: 1 cale: Standard, bazat pe dezvăluirea modulului pe baza definiției acestuia și constă într-o tranziție echivalentă la combinarea a două sisteme. │ F(x)│ =G(X)

Este rațional să se folosească această metodă în cazul unei expresii complexe pentru funcția G(x) și a unei expresii mai puțin complexe pentru funcția F(x), deoarece se presupune că rezolvă inegalitățile cu funcția F(x). 2 moduri: Constă în trecerea la un sistem echivalent în care se impune o condiție în partea dreaptă. │ F(X)│= G(X)

Această metodă este mai convenabilă de utilizat dacă expresia pentru funcția G(x) este mai puțin complicată decât pentru funcția F(x), deoarece se presupune soluția inegalității G(x) ≥ 0. În plus, în cazul din mai multe module, această metodă este recomandată pentru a utiliza a doua opțiune. Exemple: №1. Rezolvați ecuația: │x + 2│= 6 -2x
(1 sens) Răspuns: x = 1 1 / 3 №2.
│x 2 - 2x - 1 │ \u003d 2 (x + 1)
(2 sensuri) Răspuns: produsul rădăcinilor este 3.
№3. Rezolvați ecuația, în răspuns scrieți suma rădăcinilor:
│x - 6 │ \u003d x 2 - 5x + 9

Răspuns: suma rădăcinilor este 4.
Exerciții: №9. │x + 4│= - 3x №10. Rezolvați ecuația, în răspuns indicați numărul de soluții: │x 2 + x - 1 │ \u003d 2x - 1 №11 . Rezolvați ecuația, în răspuns indicați produsul rădăcinilor: │x + 3 │ \u003d x 2 + x - 6

Secțiunea 4. Ecuații de forma │F(x)│= F(x) și │F(x)│= - F(x)

Ecuațiile de acest tip sunt uneori numite „frumoase”. Deoarece partea dreaptă a ecuațiilor depinde de variabilă, există soluții dacă și numai dacă partea dreaptă este nenegativă. Prin urmare, ecuațiile inițiale sunt echivalente cu inegalitățile:
│F(x)│= F(x) F(x) ≥ 0 și │F(x)│= - F(x) F(x) Exemple: №1 . Rezolvați ecuația, în răspuns indicați rădăcina întreagă mai mică: │5x - 3│ \u003d 5x - 3 5x - 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Răspuns: x = 1№2. Rezolvați ecuația, în răspuns indicați lungimea decalajului: │x 2 - 9 │ \u003d 9 - x 2 x 2 - 9 ≤ 0 (x - 3) (x + 3) ≤ 0 [- 3; 3] Răspuns: lungimea decalajului este de 6.№3 . Rezolvați ecuația, în răspuns indicați numărul de soluții întregi: │2 + x - x 2 │ = 2 + x - x 2 2 + x - x 2 ≥ 0 x 2 - x - 2 ≤ 0 [- 1; 2] Răspuns: 4 soluții întregi.№4 . Rezolvați ecuația, în răspuns indicați cea mai mare rădăcină:
│4 - x -
│= 4 – x –
x 2 - 5x + 5 \u003d 0 D \u003d 5 x 1,2 \u003d
≈ 1,4

Răspuns: x = 3.

Exerciții: №12. Rezolvați ecuația, în răspuns indicați întreaga rădăcină: │x 2 + 6x + 8 │= x 2 + 6x + 8 №13. Rezolvați ecuația, în răspuns indicați numărul de soluții întregi: │13x - x 2 - 36│+ x 2 - 13x + 36 = 0 №14. Rezolvați ecuația, în răspuns indicați un număr întreg care nu este rădăcina ecuației:

Secțiunea 5. Ecuații de forma │F(x)│= │G(x)│

Deoarece ambele părți ale ecuației sunt nenegative, soluția implică luarea în considerare a două cazuri: expresiile submodulelor sunt egale sau opuse ca semn. Prin urmare, ecuația inițială este echivalentă cu combinația a două ecuații: │ F(X)│= │ G(X)│
Exemple: №1. Rezolvați ecuația, în răspuns indicați întreaga rădăcină: │x + 3│ \u003d │2x - 1│
Răspuns: rădăcină întreagă x = 4.№2. Rezolvați ecuația: │ x - x 2 - 1│ \u003d │2x - 3 - x 2 │
Răspuns: x = 2.№3 . Rezolvați ecuația, în răspuns indicați produsul rădăcinilor:




Rădăcinile ecuației 4x 2 + 2x - 1 \u003d 0 x 1,2 \u003d - 1±√5 / 4 Răspuns: produsul rădăcinilor este 0,25. Exerciții: №15 . Rezolvați ecuația, în răspuns indicați întreaga soluție: │x 2 - 3x + 2│ \u003d │x 2 + 6x - 1│ №16. Rezolvați ecuația, în răspuns indicați rădăcina mai mică: │5x - 3│=│7 - x│ №17 . Rezolvați ecuația, în răspuns scrieți suma rădăcinilor:

Secțiunea 6. Exemple de rezolvare a ecuațiilor nestandard

În această secțiune, luăm în considerare exemple de ecuații non-standard, în soluția cărora valoarea absolută a expresiei este relevată prin definiție. Exemple:

№1. Rezolvați ecuația, în răspuns indicați suma rădăcinilor: x │x│- 5x - 6 \u003d 0
Răspuns: suma rădăcinilor este 1 №2. . Rezolvați ecuația, în răspuns indicați rădăcina mai mică: x 2 - 4x
- 5 = 0
Răspuns: rădăcină mai mică x = - 5. №3. Rezolvați ecuația:

Răspuns: x = -1. Exerciții: №18. Rezolvați ecuația și scrieți suma rădăcinilor: x │3x + 5│= 3x 2 + 4x + 3
№19. Rezolvați ecuația: x 2 - 3x \u003d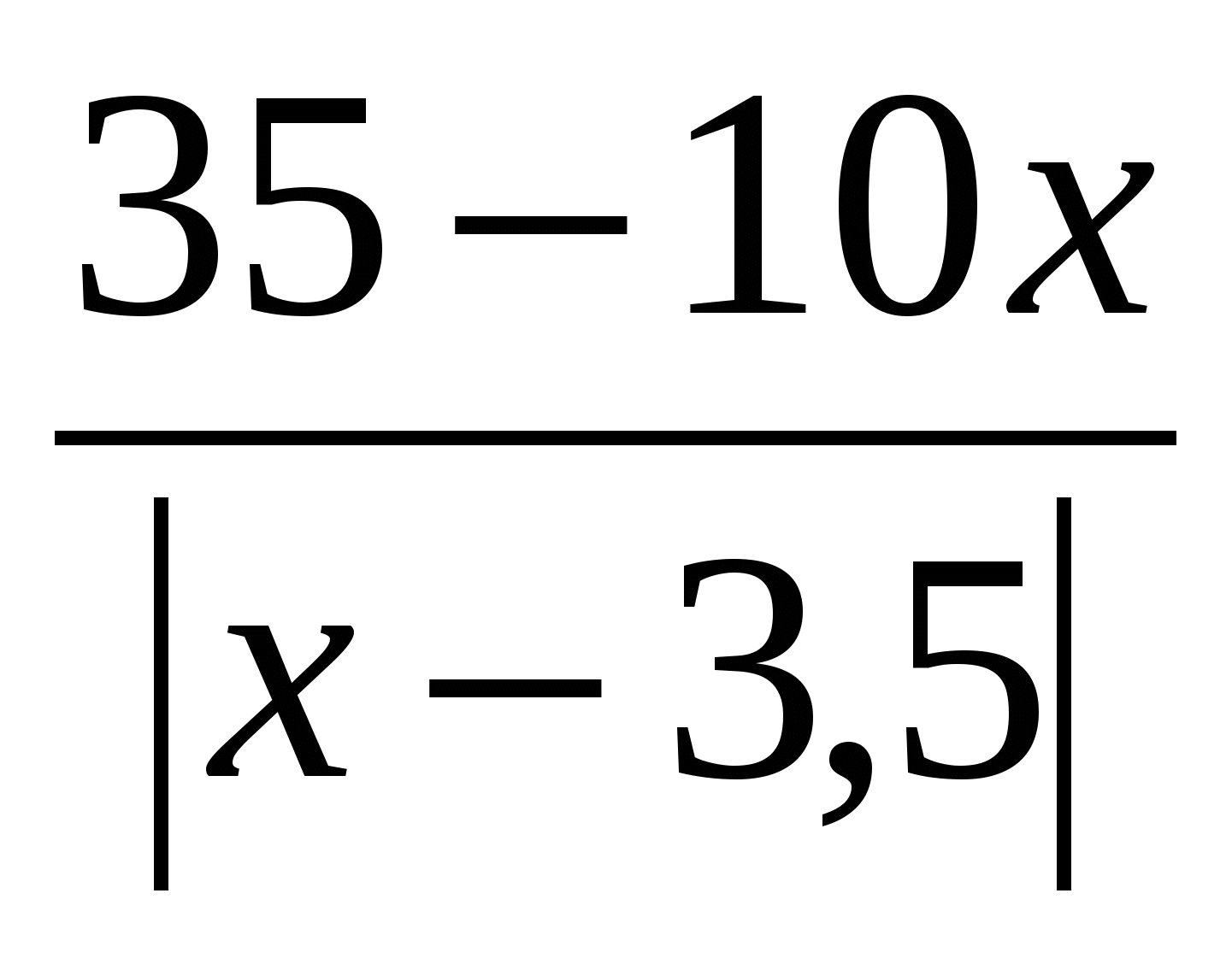

№20. Rezolvați ecuația:

Secțiunea 7. Ecuații de forma │F(x)│+│G(x)│=0

Este ușor de observat că în partea stângă a unei ecuații de acest tip, suma cantităților nenegative. Prin urmare, ecuația inițială are o soluție dacă și numai dacă ambii termeni sunt egali simultan cu zero. Ecuația este echivalentă cu sistemul de ecuații: │ F(X)│+│ G(X)│=0
Exemple: №1 . Rezolvați ecuația:
Răspuns: x = 2. №2. Rezolvați ecuația: Răspuns: x = 1. Exerciții: №21. Rezolvați ecuația: №22 . Rezolvați ecuația, în răspuns scrieți suma rădăcinilor: №23 . Rezolvați ecuația, în răspuns indicați numărul de soluții:

Secțiunea 8. Ecuații de formă

Pentru rezolvarea ecuațiilor de acest tip se folosește metoda intervalelor. Dacă se rezolvă prin extinderea secvențială a modulelor, atunci obținem n seturi de sisteme, ceea ce este foarte greoi și incomod. Luați în considerare algoritmul metodei intervalului: 1). Găsiți valori variabile X, pentru care fiecare modul este egal cu zero (zerouri ale expresiilor submodulului):
2). Valorile găsite sunt marcate pe o linie numerică, care este împărțită în intervale (numărul de intervale, respectiv, este egal cu n+1 ) 3). Stabiliți cu ce semn se dezvăluie fiecare modul la fiecare dintre intervalele obținute (când faceți o soluție, puteți folosi o linie numerică, marcând semnele pe ea) 4). Ecuația inițială este echivalentă cu mulțimea n+1 sisteme, în fiecare dintre care este indicată apartenența variabilei X unul dintre intervale. Exemple: №1 . Rezolvați ecuația, în răspuns indicați cea mai mare rădăcină:
unu). Să găsim zerourile expresiilor submodulelor: x = 2; x = -3 2). Marcam valorile găsite pe linia numerică și determinăm cu ce semn se dezvăluie fiecare modul pe intervalele obținute:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- fără soluții Ecuația are două rădăcini. Răspuns: cea mai mare rădăcină este x = 2. №2. Rezolvați ecuația, scrieți întreaga rădăcină în răspuns:
unu). Să găsim zerourile expresiilor submodulelor: x = 1,5; x = - 1 2). Marcăm valorile găsite pe linia numerică și determinăm cu ce semn se dezvăluie fiecare modul pe intervalele obținute: x + 1 x + 1 x + 1 - + +
-1 1,5 х 2х – 3 2х – 3 2х – 3 - - +
3).
Ultimul sistem nu are soluții, prin urmare, ecuația are două rădăcini. Când rezolvați ecuația, ar trebui să acordați atenție semnului „-” din fața celui de-al doilea modul. Răspuns: rădăcină întreagă x = 7. №3. Rezolvați ecuația, în răspuns indicați suma rădăcinilor: 1). Să găsim zerourile expresiilor submodulelor: x = 5; x = 1; x = - 2 2). Marcăm valorile găsite pe linia numerică și determinăm cu ce semn se dezvăluie fiecare modul pe intervalele obținute: x - 5 x - 5 x - 5 x - 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Ecuația are două rădăcini x = 0 și 2. Răspuns: suma rădăcinilor este 2. №4 . Rezolvați ecuația: 1). Să găsim zerourile expresiilor submodulelor: x = 1; x = 2; x = 3. 2). Să determinăm semnul cu care fiecare modul este extins pe intervalele obținute. 3).
Să combinăm soluțiile primei trei sisteme. Răspuns: ; x = 5.
Exerciții: №24. Rezolvați ecuația:
№25. Rezolvați ecuația, în răspuns scrieți suma rădăcinilor: №26. Rezolvați ecuația, în răspuns indicați rădăcina mai mică: №27. Rezolvați ecuația, dați rădăcina mai mare în răspunsul dvs.:

Secțiunea 9. Ecuații care conțin module multiple

Ecuațiile care conțin mai multe module presupun prezența valorilor absolute în expresiile submodulelor. Principiul de bază al rezolvării ecuațiilor de acest tip este dezvăluirea secvențială a modulelor, începând cu cele „externe”. În cursul soluției se folosesc tehnicile discutate în secțiunile nr. 1, nr. 3.

Exemple: №1. Rezolvați ecuația:
Răspuns: x = 1; - unsprezece. №2. Rezolvați ecuația:
Răspuns: x = 0; patru; - patru. №3. Rezolvați ecuația, în răspuns indicați produsul rădăcinilor:
Răspuns: produsul rădăcinilor este 8. №4. Rezolvați ecuația:
Notați ecuațiile populației (1) și (2) și luați în considerare soluția fiecăruia dintre ele separat pentru comoditatea designului. Deoarece ambele ecuații conțin mai mult de un modul, este mai convenabil să se efectueze o tranziție echivalentă la seturi de sisteme. (1)

(2)


Răspuns:
Exerciții: №36. Rezolvați ecuația, în răspuns indicați suma rădăcinilor: 5 │3x-5│ \u003d 25 x №37. Rezolvați ecuația, dacă sunt mai multe rădăcini, în răspuns indicați suma rădăcinilor: │x + 2│ x - 3x - 10 = 1 №38. Rezolvați ecuația: 3 │2x -4│ \u003d 9 │x│ №39. Rezolvați ecuația, în răspuns indicați numărul de rădăcini pentru: 2 │ sin x │ = √2 №40 . Rezolvați ecuația, în răspuns indicați numărul de rădăcini:

Secțiunea 3. Ecuații logaritmice.

Înainte de a rezolva următoarele ecuații, este necesar să trecem în revistă proprietățile logaritmilor și ale funcției logaritmice. Exemple: №1. Rezolvați ecuația, în răspuns indicați produsul rădăcinilor: log 2 (x + 1) 2 + log 2 │x + 1 │ \u003d 6 O.D.Z. x+1≠0 x≠ - 1

Cazul 1: dacă x ≥ - 1, atunci log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – satisface condiția x ≥ - 1 2 caz: dacă x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – satisface condiția x - 1
Răspuns: produsul rădăcinilor este 15.
№2. Rezolvați ecuația, în răspuns indicați suma rădăcinilor: lg
O.D.Z.

Răspuns: suma rădăcinilor este 0,5.
№3. Rezolvați ecuația: log 5
O.D.Z.

Răspuns: x = 9. №4. Rezolvați ecuația: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Să folosim formula pentru a trece la o altă bază. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Să ​​aflăm zerourile expresiilor submodulelor: x = 25; x \u003d Aceste numere împart aria valorilor permise în trei intervale, astfel încât ecuația este echivalentă cu totalitatea a trei sisteme.
Răspuns: )