Kas yra skalės trikampio apibrėžimas. Kas yra trikampis. Kokie jie yra. Trikampis – apibrėžimas ir bendrosios sąvokos

Šiandien vykstame į Geometrijos šalį, kur susipažinsime su įvairių tipų trikampiais.

Išnagrinėkite geometrines figūras ir raskite tarp jų „papildomą“ (1 pav.).

Ryžiai. 1. Pavyzdžiui, iliustracija

Matome, kad skaičiai Nr. 1, 2, 3, 5 yra keturkampiai. Kiekvienas iš jų turi savo pavadinimą (2 pav.).

Ryžiai. 2. Keturkampiai

Tai reiškia, kad „papildoma“ figūra yra trikampis (3 pav.).

Ryžiai. 3. Pavyzdžiui, iliustracija

Trikampis yra figūra, kurią sudaro trys taškai, kurie nėra toje pačioje tiesėje, ir trys linijos atkarpos, jungiančios šiuos taškus poromis.

Taškai vadinami trikampio viršūnės, segmentai - jo vakarėliams. Susiformuoja trikampio kraštinės Trikampio viršūnėse yra trys kampai.

Pagrindinės trikampio savybės yra trys šonai ir trys kampai. Trikampiai klasifikuojami pagal kampą aštrus, stačiakampis ir bukas.

Trikampis vadinamas smailiuoju, jei visi trys jo kampai yra smailieji, tai yra mažesni nei 90° (4 pav.).

Ryžiai. 4. Smailus trikampis

Trikampis vadinamas stačiu kampu, jei vienas jo kampas yra 90° (5 pav.).

Ryžiai. 5. Statusis trikampis

Trikampis vadinamas buku, jei vienas iš jo kampų yra bukas, t.y. didesnis nei 90° (6 pav.).

Ryžiai. 6. Bukas trikampis

Pagal lygių kraštinių skaičių trikampiai yra lygiakraščiai, lygiašoniai, skalės.

Lygiašonis trikampis yra trikampis, kurio dvi kraštinės lygios (7 pav.).

Ryžiai. 7. Lygiašonis trikampis

Šios pusės vadinamos šoninis, Trečioji pusė - pagrindu. Lygiašonio trikampio kampai prie pagrindo yra lygūs.

Lygiašoniai trikampiai yra ūmus ir bukas(8 pav.) .

Ryžiai. 8. Smailieji ir bukieji lygiašoniai trikampiai

Vadinamas lygiakraštis trikampis, kurio visos trys kraštinės lygios (9 pav.).

Ryžiai. 9. Lygiakraštis trikampis

Lygiakraščiame trikampyje visi kampai lygūs. Lygiakraščiai trikampiai visada smailaus kampo.

Universaliu vadinamas trikampis, kurio visos trys kraštinės yra skirtingo ilgio (10 pav.).

Ryžiai. 10. Skaleninis trikampis

Atlikite užduotį. Padalinkite šiuos trikampius į tris grupes (11 pav.).

Ryžiai. 11. Užduoties iliustracija

Pirma, paskirstykime pagal kampų dydį.

Smailūs trikampiai: Nr.1, Nr.3.

Statieji trikampiai: #2, #6.

Bukieji trikampiai: #4, #5.

Šie trikampiai skirstomi į grupes pagal lygių kraštinių skaičių.

Skaleniniai trikampiai: Nr.4, Nr.6.

Lygiašoniai trikampiai: Nr.2, Nr.3, Nr.5.

Lygiakraštis trikampis: Nr. 1.

Peržiūrėkite brėžinius.

Pagalvokite, iš kokios vielos gabalo pagamintas kiekvienas trikampis (12 pav.).

Ryžiai. 12. Užduoties iliustracija

Galite ginčytis taip.

Pirmasis vielos gabalas padalintas į tris lygias dalis, todėl iš jo galite padaryti lygiakraštį trikampį. Paveiksle jis parodytas trečias.

Antroji vielos dalis yra padalinta į tris skirtingas dalis, todėl iš jos galite padaryti skaleno trikampį. Nuotraukoje jis parodytas pirmiausia.

Trečias vielos gabalas padalintas į tris dalis, kur dvi dalys yra vienodo ilgio, todėl iš jos galite padaryti lygiašonį trikampį. Jis parodytas antras paveikslėlyje.

Šiandien pamokoje susipažinome su įvairių tipų trikampiais.

Bibliografija

1. M.I. Moro, M.A. Bantova ir kt.. Matematika: vadovėlis. 3 klasė: iš 2 dalių, 1 dalis. - M .: "Švietimas", 2012 m.
2. M.I. Moro, M.A. Bantova ir kt.. Matematika: vadovėlis. 3 klasė: iš 2 dalių, 2 dalis. - M .: "Švietimas", 2012 m.
3. M.I. Moreau. Matematikos pamokos: gairės mokytojams. 3 klasė - M.: Švietimas, 2012 m.
4. Reguliavimo dokumentas. Mokymosi rezultatų stebėjimas ir vertinimas. - M.: „Švietimas“, 2011 m.
5. „Rusijos mokykla“: programos pradinei mokyklai. - M.: „Švietimas“, 2011 m.
6. S.I. Volkovas. Matematika: Testinis darbas. 3 klasė - M.: Švietimas, 2012 m.
7. V.N. Rudnickaja. Testai. - M.: „Egzaminas“, 2012 m.

1. Nsportal.ru ().
2. Prosv.ru ().
3. Do.gendocs.ru ().

Namų darbai

1. Užbaikite frazes.

a) Trikampis yra figūra, sudaryta iš ..., esanti ne vienoje tiesėje, ir ..., jungianti šiuos taškus poromis.

b) Taškai vadinami … , segmentai - jo … . Trikampio kraštinės susidaro trikampio viršūnėse ….

c) Pagal kampo dydį trikampiai yra ..., ..., ....

d) Pagal lygių kraštinių skaičių trikampiai yra ..., ..., ....

2. Pieškite

a) stačiakampis trikampis

b) smailusis trikampis;

c) bukas trikampis;

d) lygiakraštis trikampis;

e) skalės trikampis;

e) lygiašonis trikampis.

3. Pamokos tema padarykite užduotį savo bendražygiams.

Šiandien vykstame į Geometrijos šalį, kur susipažinsime su įvairių tipų trikampiais.

Išnagrinėkite geometrines figūras ir raskite tarp jų „papildomą“ (1 pav.).

Ryžiai. 1. Pavyzdžiui, iliustracija

Matome, kad skaičiai Nr. 1, 2, 3, 5 yra keturkampiai. Kiekvienas iš jų turi savo pavadinimą (2 pav.).

Ryžiai. 2. Keturkampiai

Tai reiškia, kad „papildoma“ figūra yra trikampis (3 pav.).

Ryžiai. 3. Pavyzdžiui, iliustracija

Trikampis yra figūra, kurią sudaro trys taškai, kurie nėra toje pačioje tiesėje, ir trys linijos atkarpos, jungiančios šiuos taškus poromis.

Taškai vadinami trikampio viršūnės, segmentai - jo vakarėliams. Susiformuoja trikampio kraštinės Trikampio viršūnėse yra trys kampai.

Pagrindinės trikampio savybės yra trys šonai ir trys kampai. Trikampiai klasifikuojami pagal kampą aštrus, stačiakampis ir bukas.

Trikampis vadinamas smailiuoju, jei visi trys jo kampai yra smailieji, tai yra mažesni nei 90° (4 pav.).

Ryžiai. 4. Smailus trikampis

Trikampis vadinamas stačiu kampu, jei vienas jo kampas yra 90° (5 pav.).

Ryžiai. 5. Statusis trikampis

Trikampis vadinamas buku, jei vienas iš jo kampų yra bukas, t.y. didesnis nei 90° (6 pav.).

Ryžiai. 6. Bukas trikampis

Pagal lygių kraštinių skaičių trikampiai yra lygiakraščiai, lygiašoniai, skalės.

Lygiašonis trikampis yra trikampis, kurio dvi kraštinės lygios (7 pav.).

Ryžiai. 7. Lygiašonis trikampis

Šios pusės vadinamos šoninis, Trečioji pusė - pagrindu. Lygiašonio trikampio kampai prie pagrindo yra lygūs.

Lygiašoniai trikampiai yra ūmus ir bukas(8 pav.) .

Ryžiai. 8. Smailieji ir bukieji lygiašoniai trikampiai

Vadinamas lygiakraštis trikampis, kurio visos trys kraštinės lygios (9 pav.).

Ryžiai. 9. Lygiakraštis trikampis

Lygiakraščiame trikampyje visi kampai lygūs. Lygiakraščiai trikampiai visada smailaus kampo.

Universaliu vadinamas trikampis, kurio visos trys kraštinės yra skirtingo ilgio (10 pav.).

Ryžiai. 10. Skaleninis trikampis

Atlikite užduotį. Padalinkite šiuos trikampius į tris grupes (11 pav.).

Ryžiai. 11. Užduoties iliustracija

Pirma, paskirstykime pagal kampų dydį.

Smailūs trikampiai: Nr.1, Nr.3.

Statieji trikampiai: #2, #6.

Bukieji trikampiai: #4, #5.

Šie trikampiai skirstomi į grupes pagal lygių kraštinių skaičių.

Skaleniniai trikampiai: Nr.4, Nr.6.

Lygiašoniai trikampiai: Nr.2, Nr.3, Nr.5.

Lygiakraštis trikampis: Nr. 1.

Peržiūrėkite brėžinius.

Pagalvokite, iš kokios vielos gabalo pagamintas kiekvienas trikampis (12 pav.).

Ryžiai. 12. Užduoties iliustracija

Galite ginčytis taip.

Pirmasis vielos gabalas padalintas į tris lygias dalis, todėl iš jo galite padaryti lygiakraštį trikampį. Paveiksle jis parodytas trečias.

Antroji vielos dalis yra padalinta į tris skirtingas dalis, todėl iš jos galite padaryti skaleno trikampį. Nuotraukoje jis parodytas pirmiausia.

Trečias vielos gabalas padalintas į tris dalis, kur dvi dalys yra vienodo ilgio, todėl iš jos galite padaryti lygiašonį trikampį. Jis parodytas antras paveikslėlyje.

Šiandien pamokoje susipažinome su įvairių tipų trikampiais.

Bibliografija

1. M.I. Moro, M.A. Bantova ir kt.. Matematika: vadovėlis. 3 klasė: iš 2 dalių, 1 dalis. - M .: "Švietimas", 2012 m.
2. M.I. Moro, M.A. Bantova ir kt.. Matematika: vadovėlis. 3 klasė: iš 2 dalių, 2 dalis. - M .: "Švietimas", 2012 m.
3. M.I. Moreau. Matematikos pamokos: gairės mokytojams. 3 klasė - M.: Švietimas, 2012 m.
4. Reguliavimo dokumentas. Mokymosi rezultatų stebėjimas ir vertinimas. - M.: „Švietimas“, 2011 m.
5. „Rusijos mokykla“: programos pradinei mokyklai. - M.: „Švietimas“, 2011 m.
6. S.I. Volkovas. Matematika: Testinis darbas. 3 klasė - M.: Švietimas, 2012 m.
7. V.N. Rudnickaja. Testai. - M.: „Egzaminas“, 2012 m.

1. Nsportal.ru ().
2. Prosv.ru ().
3. Do.gendocs.ru ().

Namų darbai

1. Užbaikite frazes.

a) Trikampis yra figūra, sudaryta iš ..., esanti ne vienoje tiesėje, ir ..., jungianti šiuos taškus poromis.

b) Taškai vadinami … , segmentai - jo … . Trikampio kraštinės susidaro trikampio viršūnėse ….

c) Pagal kampo dydį trikampiai yra ..., ..., ....

d) Pagal lygių kraštinių skaičių trikampiai yra ..., ..., ....

2. Pieškite

a) stačiakampis trikampis

b) smailusis trikampis;

c) bukas trikampis;

d) lygiakraštis trikampis;

e) skalės trikampis;

e) lygiašonis trikampis.

3. Pamokos tema padarykite užduotį savo bendražygiams.

Standartiniai užrašai

Trikampis su viršūnėmis A, B Ir Cžymimas kaip (žr. pav.). Trikampis turi tris kraštines:

Trikampio kraštinių ilgiai žymimi mažosiomis lotyniškomis raidėmis (a, b, c):

Trikampis turi šiuos kampus:

Kampai atitinkamose viršūnėse tradiciškai žymimi graikiškomis raidėmis (α, β, γ).

Trikampių lygybės ženklai

Trikampis Euklido plokštumoje gali būti vienareikšmiškai (iki kongruencijos) apibrėžtas šiais pagrindinių elementų trynukais:

1. a, b, γ (dviejų kraštų lygybė ir kampas tarp jų);
2. a, β, γ (šoninių ir dviejų gretimų kampų lygybė);
3. a, b, c (lygybė iš trijų pusių).

Stačiųjų trikampių lygybės ženklai:

1. išilgai kojos ir hipotenuzės;
2. ant dviejų kojų;
3. išilgai kojos ir ūmaus kampo;
4. hipotenuzė ir ūminis kampas.

Kai kurie trikampio taškai yra „suporuoti“. Pavyzdžiui, yra du taškai, iš kurių visos pusės matomos arba 60° kampu, arba 120° kampu. Jie vadinami taškais Torricelli. Taip pat yra du taškai, kurių projekcijos šonuose yra taisyklingo trikampio viršūnėse. tai - Apolonijaus taškai. Taškai ir tokie kaip vadinami Brocard taškai.

Tiesioginis

Bet kuriame trikampyje svorio centras, ortocentras ir apibrėžto apskritimo centras yra toje pačioje tiesėje, vadinamoje Eulerio linija.

Tiesė, einanti per apibrėžtojo apskritimo centrą ir Lemoine tašką, vadinama Brokaro ašis. Ant jo guli Apolonijaus taškai. Torricelli taškai ir Lemoine taškai taip pat yra toje pačioje tiesėje. Trikampio kampų išorinių pusių pagrindai yra toje pačioje tiesėje, vadinamoje išorinių bisektorių ašis. Tiesių, kuriose yra stačiakampio kraštinės, susikirtimo taškai su linijomis, kuriose yra trikampio kraštinės, taip pat yra toje pačioje tiesėje. Ši linija vadinama ortocentrinė ašis, jis yra statmenas Eilerio linijai.

Jei paimsime tašką ant trikampio apibrėžtojo apskritimo, tai jo projekcijos trikampio kraštinėse bus vienoje tiesėje, vadinamoje Simsono tiesioji linija duotas taškas. Diametraliai priešingų taškų Simsono linijos yra statmenos.

trikampiai

• Vadinamas trikampis, kurio viršūnės yra per tam tikrą tašką nubrėžtų cevijų pagrindų cevijaus trikampisšį tašką.
• Vadinamas trikampis, kurio viršūnės yra tam tikro taško projekcijose į šonus po oda arba pedalo trikampisšį tašką.
• Trikampis, kurio viršūnės yra antruosiuose tiesių, nubrėžtų per viršūnes ir duotąjį tašką, susikirtimo taškuose su apibrėžtuoju apskritimu, vadinamas cevijaus trikampis. Cevijos trikampis yra panašus į poodinį trikampį.

apskritimai

• Įrašytas apskritimas yra apskritimas, kurio liestinė yra visos trys trikampio kraštinės. Ji vienintelė. Įbrėžto apskritimo centras vadinamas centre.
• Apribotas ratas- apskritimas, einantis per visas tris trikampio viršūnes. Apribotas ratas taip pat yra unikalus.
• Išskleisti aplinką- apskritimas, liečiantis vieną trikampio kraštinę, ir kitų dviejų kraštinių tęsinys. Trikampyje yra trys tokie apskritimai. Jų radikalus centras yra įbrėžto vidurinio trikampio apskritimo centras, vadinamas Spiekerio mintis.

Trikampio trijų kraštinių vidurio taškai, jo trijų aukščių pagrindai ir trijų tiesių atkarpų, jungiančių trikampio viršūnes su ortocentru, vidurio taškai yra viename apskritime, vadinamame devynių taškų ratas arba Eulerio ratas. Devynių taškų apskritimo centras yra ant Eilerio linijos. Devynių taškų apskritimas liečia įbrėžtą apskritimą ir tris apskritimus. Įbrėžto apskritimo ir devynių taškų apskritimo sąlyčio taškas vadinamas Feuerbacho taškas. Jei iš kiekvienos viršūnės tiesiame trikampius tiesiose linijose, turinčiose kraštines, ortezes, kurių ilgis lygus priešingoms kraštinėms, tada gauti šeši taškai yra viename apskritime - Conway apskritimai. Bet kuriame trikampyje trys apskritimai gali būti įrašyti taip, kad kiekvienas iš jų liestų dvi trikampio kraštines ir du kitus apskritimus. Tokie apskritimai vadinami Malfatti apskritimai. Šešių trikampių, į kuriuos trikampis padalintas medianomis, apibrėžtųjų apskritimų centrai yra viename apskritime, kuris vadinamas Lamuno ratas.

Trikampis turi tris apskritimus, kurie liečia dvi trikampio ir apibrėžtojo apskritimo kraštines. Tokie apskritimai vadinami pusiau užrašytas arba Verrier apskritimai. Atkarpos, jungiančios Verrier apskritimų sąlyčio taškus su apibrėžtuoju apskritimu, susikerta viename taške, vadinamame Verrier taškas. Jis tarnauja kaip homotetikos centras, kuris nukelia apibrėžtą apskritimą į apskritimą. Verrier apskritimų ir kraštinių liesties taškai yra tiesėje, kuri eina per įbrėžto apskritimo centrą.

Tiesijos atkarpos, jungiančios įbrėžto apskritimo liestinės taškus su viršūnėmis, susikerta viename taške, vadinamame Gergonne tašką, o atkarpas, jungiančias viršūnes su išorinių apskritimų sąlyčio taškais – į Nagel taškas.

Elipsės, parabolės ir hiperbolės

Įbrėžtas kūgis (elipsė) ir jo perspektyva

Į trikampį galima įrašyti begalinį skaičių kūgių (elipsių, parabolių arba hiperbolių). Jei į trikampį įrašysime savavališką kūgį ir sujungsime sąlyčio taškus su priešingomis viršūnėmis, tai gautos linijos susikirs viename taške, vadinamame perspektyvą kūginiai. Bet kuriame plokštumos taške, kuris nėra ant šono ar jo tęsinio, yra įbrėžtas kūgis su perspektyva tame taške.

Steinerio elipsė apribota ir per jos židinius einantys ceviai

Elipsė gali būti įrašyta į trikampį, kuris liečia kraštines vidurio taškuose. Tokia elipsė vadinama Steinerio įrašyta elipsė(jo perspektyva bus trikampio centroidas). Apibūdinta elipsė, kuri yra liestinė tiesių, einančių per viršūnes lygiagrečiai kraštams, vadinama apribotas Šteinerio elipsės. Jei afininė transformacija ("kreipimas") paverčia trikampį taisyklingu, tada jo įrašyta ir apibrėžta Steinerio elipsė pateks į įbrėžtą ir apibrėžtą apskritimą. Cevians, nubrėžtos per aprašytos Šteinerio elipsės židinius (Skutino taškai), yra lygūs (Skutino teorema). Iš visų aprašytų elipsių aprašytoji Šteinerio elipsė turi mažiausią plotą, o iš visų užrašytų elipsių – didžiausią plotą.

Brokaro elipsė ir jos žvalgytojas – Lemoine taškas

Vadinama elipsė su židiniais Brokaro taškuose Brocard elipsė. Jo perspektyva yra Lemoine taškas.

Įbrėžtos parabolės savybės

Kieperto parabolė

Įrašytų parabolių perspektyvos guli ant apribotos Steinerio elipsės. Įbrėžtos parabolės židinys yra ant apibrėžto apskritimo, o kryptis eina per ortocentrą. Vadinama parabolė, įrašyta į trikampį, kurio kryptis yra Eulerio linija Kieperto parabolė. Jo perspektyva yra ketvirtasis apibrėžtojo apskritimo ir apibrėžtosios Šteinerio elipsės susikirtimo taškas, vadinamas Steinerio taškas.

Kiperto hiperbolė

Jei aprašyta hiperbolė eina per aukščių susikirtimo tašką, tada ji yra lygiakraštė (tai yra, jos asimptotės yra statmenos). Lygiakraščio hiperbolės asimptotų susikirtimo taškas yra devynių taškų apskritime.

Transformacijos

Jeigu tiesės, einančios per viršūnes ir kurį nors šonuose negulantį tašką ir jų plėtinius, atsispindės atitinkamų bisektorių atžvilgiu, tai jų atvaizdai taip pat susikirs viename taške, kuris vadinamas izogoniškai konjuguotas originalus (jei taškas yra ant apibrėžto apskritimo, tada gautos linijos bus lygiagrečios). Daugelis žymių taškų porų yra izogoniškai susijungusios: apibrėžto apskritimo centras ir ortocentras, centroidas ir Lemoine taškas, Brokaro taškai. Apolonijaus taškai yra izogoniškai konjuguoti su Torricelli taškais, o apskritimo centras yra izogoniškai susietas su pačiu savimi. Veikiant izogoninei konjugacijai, tiesios linijos pereina į apibrėžtuosius kūgius, o apribotos kūgius į tiesias linijas. Taigi Kieperto hiperbolė ir Brokaro ašis, Enžabeko hiperbolė ir Eilerio linija, Feuerbacho hiperbolė ir įbrėžto apskritimo centrų linija yra izogoniškai konjuguotos. Izogoniškai susietų taškų subderminių trikampių apibrėžtieji apskritimai sutampa. Įrašytų elipsių židiniai yra izogoniškai susijungę.

Jei vietoj simetrinio ceviano imsime cevianą, kurio pagrindas yra taip toli nuo šono vidurio, kaip ir pradinio pagrindo, tai tokie cevianai taip pat susikirs viename taške. Gauta transformacija vadinama izotominė konjugacija. Jis taip pat susieja linijas su apibrėžtais kūgiais. Gergonne ir Nagel taškai yra izotomiškai konjuguoti. Afininių transformacijų metu izotomiškai konjuguoti taškai pereina į izotomiškai konjuguotus. Izotomijos konjugacijos metu aprašyta Steinerio elipsė eina į tiesią liniją begalybėje.

Jei atkarpose, kurias trikampio kraštinės atskiria nuo apibrėžtojo apskritimo, įbrėžiami apskritimai, kurie liečiasi per tam tikrą tašką nubrėžtų cevijų pagrindų kraštines, o tada šių apskritimų sąlyčio taškai sujungiami su apibrėžtuoju apskritimas su priešingomis viršūnėmis, tada tokios tiesės susikirs viename taške. Vadinama plokštumos transformacija, suderinant pradinį tašką su gautuoju izocirkuliacinė transformacija. Izogoninių ir izotominių konjugacijų sudėtis yra izocirkuliarinės transformacijos su savimi kompozicija. Ši kompozicija yra projekcinė transformacija, kuri palieka trikampio kraštines vietoje, o išorinių bisektorių ašis paverčia tiesia linija begalybėje.

Jei tęsime kokio nors taško Ceviano trikampio kraštines ir paimsime jų susikirtimo taškus su atitinkamomis kraštinėmis, tada susikirtimo taškai bus vienoje tiesėje, vadinamoje trilinijinis poliarinis atspirties taškas. Ortocentrinė ašis – trilinijinė ortocentro poliarinė; įbrėžto apskritimo centro tritiesė poliarinė yra išorinių bisektorių ašis. Taškų, esančių ant apibrėžtojo kūgio, tritiesės poliai susikerta viename taške (apibrėžtajam apskritimui tai yra Lemoine taškas, apibrėžtajai Steinerio elipsei - centroidas). Izogoninės (arba izotominės) konjugacijos ir tritiesės poliarinės konjugacijos sudėtis yra dvilypė transformacija (jei taškas, sujungtas izogoniškai (izotomiškai) su tašku, yra ant taško tritiesės poliarinės linijos, tada taško trilinijinis polius izogoniškai (izotomiškai) konjugatas su tašku yra taško tritiesėje poliarinėje ).

Kubeliai

Santykiai trikampyje

Pastaba:Šiame skyriuje, , , yra trijų trikampio kraštinių ilgiai, ir , yra kampai, esantys atitinkamai priešais šias tris puses (priešingi kampai).

trikampio nelygybė

Neišsigimusiame trikampyje jo dviejų kraštinių ilgių suma yra didesnė už trečiosios kraštinės ilgį, išsigimusiame – lygi. Kitaip tariant, trikampio kraštinių ilgiai yra susieti su šiomis nelygybėmis:

Trikampio nelygybė yra viena iš metrikos aksiomų.

Trikampio kampų sumos teorema

Sinuso teorema

,

čia R yra apskritimo, apibrėžiamo aplink trikampį, spindulys. Iš teoremos išplaukia, kad jei a< b < c, то α < β < γ.

Kosinuso teorema

Tangento teorema

Kiti santykiai

Metriniai santykiai trikampyje pateikiami:

Trikampių sprendimas

Nežinomų trikampio kraštinių ir kampų skaičiavimas, remiantis žinomomis, istoriškai buvo vadinamas „trikampio sprendiniais“. Šiuo atveju naudojamos aukščiau pateiktos bendrosios trigonometrinės teoremos.

Trikampio plotas

Ypatingi atvejai Žymėjimas

Šioje srityje galioja šios nelygybės:

Trikampio ploto erdvėje apskaičiavimas naudojant vektorius

Tegul trikampio viršūnės yra taškuose , , .

Įveskime ploto vektorių . Šio vektoriaus ilgis lygus trikampio plotui ir nukreiptas išilgai normalios trikampio plokštumos:

Leisti , Kur , , yra trikampio projekcijos į koordinačių plokštumas. Kuriame

ir taip pat

Trikampio plotas yra.

Alternatyva yra apskaičiuoti kraštinių ilgius (naudojant Pitagoro teoremą) ir tada naudojant Herono formulę.

Trikampio teoremos

Ši dalis nebaigta.

Iš visų daugiakampių trikampiai turi mažiausią kampų ir šonų skaičių.

Trikampius galima atskirti pagal jų kampų formą.

Jei visi trikampio kampai yra smailieji, tada jis vadinamas smailiuoju trikampiu.(113 pav., a).

Jei vienas iš trikampio kampų yra stačiakampis, tada jis vadinamas stačiu trikampiu.(113 pav., b).

Jei vienas iš trikampio kampų yra bukas, tada jis vadinamas buku trikampiu.(113 pav., c).

Jie sako, kad mes klasifikuojami trikampiai pagal jų kampus.

Trikampius galima klasifikuoti ne tik pagal kampų tipą, bet ir pagal lygių kraštinių skaičių.

Jei dvi trikampio kraštinės yra lygios, tada jis vadinamas lygiašoniu trikampiu.

114 paveiksle a pavaizduotas lygiašonis trikampis ABC, kuriame AB \u003d BC. Paveiksle lygios kraštinės pažymėtos vienodu brūkšnelių skaičiumi. Vadinamos lygios kraštinės AB ir BC pusės, o šoninė AC − pagrindu lygiašonis trikampis ABC.

Jei trikampio kraštinės yra lygios, tada jis vadinamas lygiakraštiu trikampiu.

114b paveiksle parodytas trikampis yra lygiakraštis, jo MN = NE = EM.

Trikampis su trimis skirtingo ilgio kraštinėmis vadinamas skalės trikampiu.

113 paveiksle pavaizduoti trikampiai yra masteliniai. Jei lygiakraščio trikampio kraštinė yra a, tada jo perimetras apskaičiuojamas pagal formulę:

P = 3a

Pavyzdys 1 . Naudodami liniuotę ir transporterį sukonstruokite trikampį, kurio dvi kraštinės yra 3 cm ir 2 cm, o kampas tarp jų yra 50°.

Naudodami transporterį sukonstruosime kampą A, kurio laipsnio matas yra 50 ° (115 pav.). Šio kampo šonuose nuo jo viršūnės liniuote atidėkite 3 cm ilgio atkarpą AB ir 2 cm ilgio atkarpą AC (116 pav.). Sujungdami taškus B ir C su atkarpa, gauname norimą trikampį ABC ( 117 pav.).

Pavyzdys 2 . Naudodami liniuotę ir transporterį, sukonstruokite trikampį ABC, kurio kraštinė AB yra 2 cm, o kampai CAB ir CBA yra atitinkamai 40° ir 110°.

Sprendimas. Liniuote statome 2 cm ilgio atkarpą AB ( 118 pav.). Iš sijos AB, naudodami transporterį, taške A nustatome kampą su viršūne, kurio laipsnio matas yra 40 °. Nuo spindulio BA ta pačia kryptimi nuo tiesės AB, kurioje buvo nubrėžtas pirmasis kampas, atimame kampą su viršūne taške B, kurio laipsnio matas yra 110 ° (119 pav.).

Radę kampų A ir B kraštinių susikirtimo tašką C, gauname norimą trikampį ABC (120 pav.).

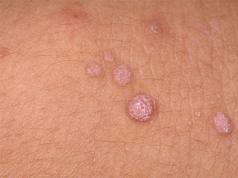
Net ikimokyklinio amžiaus vaikai žino, kaip atrodo trikampis. Bet kokie jie yra, vaikinai jau pradeda suprasti mokykloje. Vienas tipas yra bukas trikampis. Norėdami suprasti, kas tai yra, paprasčiausias būdas yra pamatyti paveikslėlį su jo atvaizdu. Ir teoriškai tai yra tai, ką jie vadina „paprasčiausiu daugiakampiu“ su trimis kraštinėmis ir viršūnėmis, iš kurių viena yra

Sąvokų supratimas

Geometrijoje yra tokių tipų figūros su trimis kraštinėmis: smailus, stačiakampis ir bukas trikampis. Be to, šių paprasčiausių daugiakampių savybės yra vienodos visiems. Taigi visoms išvardytoms rūšims tokia nelygybė bus stebima. Bet kurių dviejų kraštinių ilgių suma būtinai yra didesnė už trečiosios kraštinės ilgį.

Tačiau norint įsitikinti, kad kalbame apie pilną figūrą, o ne apie atskirų viršūnių aibę, reikia patikrinti, ar tenkinama pagrindinė sąlyga: bukojo trikampio kampų suma yra 180 o. Tas pats pasakytina ir apie kitų tipų figūras su trimis kraštais. Tiesa, bukajame trikampyje vienas iš kampų bus net didesnis nei 90 o, o likę du būtinai aštrūs. Šiuo atveju tai yra didžiausias kampas, kuris bus priešais ilgiausią kraštą. Tiesa, tai toli gražu ne visos buko trikampio savybės. Tačiau net ir žinodami tik šias savybes, mokiniai gali išspręsti daugybę geometrijos uždavinių.

Kiekvienam daugiakampiui, turinčiam tris viršūnes, taip pat tiesa, kad tęsdami bet kurią iš kraštinių gauname kampą, kurio dydis bus lygus dviejų negretimų vidinių viršūnių sumai. Bukojo trikampio perimetras apskaičiuojamas taip pat, kaip ir kitų formų. Jis lygus visų jo kraštinių ilgių sumai. Norint nustatyti matematikus, buvo išvestos įvairios formulės, priklausomai nuo to, kokie duomenys buvo iš pradžių.

Teisingas stilius

Viena iš svarbiausių geometrijos uždavinių sprendimo sąlygų yra teisingas brėžinys. Matematikos mokytojai dažnai sako, kad tai padės ne tik įsivaizduoti, kas duota ir ko iš jūsų reikalaujama, bet ir 80% priartėti prie teisingo atsakymo. Štai kodėl svarbu žinoti, kaip sukurti bukąjį trikampį. Jei norite tik hipotetinės figūros, galite nubrėžti bet kurį daugiakampį su trimis kraštinėmis, kad vienas iš kampų būtų didesnis nei 90 laipsnių.

Jei pateikiamos tam tikros kraštinių ilgių ar kampų laipsnių reikšmės, pagal jas reikia nubraižyti bukukampį trikampį. Tuo pačiu reikia stengtis kuo tiksliau pavaizduoti kampus, juos apskaičiuojant transporterio pagalba, o šonus atvaizduoti proporcingai užduotyje pateiktoms sąlygoms.

Pagrindinės linijos

Dažnai moksleiviams nepakanka tik žinoti, kaip turi atrodyti tam tikros figūros. Jie negali apsiriboti informacija apie tai, kuris trikampis yra bukas, o kuris stačiakampis. Matematikos kursas numato, kad jų žinios apie pagrindines figūrų savybes turėtų būti išsamesnės.

Taigi, kiekvienas mokinys turėtų suprasti pusiausvyros, medianos, statmeno bisektoriaus ir aukščio apibrėžimą. Be to, jis turi žinoti pagrindines jų savybes.

Taigi, bisektoriniai padalija kampą per pusę, o priešingą pusę - į segmentus, kurie yra proporcingi gretimoms kraštinėms.

Mediana padalija bet kurį trikampį į dvi lygias sritis. Toje vietoje, kurioje jie susikerta, kiekvienas iš jų yra padalintas į 2 segmentus santykiu 2: 1, žiūrint iš viršaus, iš kurio jis kilo. Šiuo atveju didžiausia mediana visada traukiama į mažiausią jos pusę.

Ne mažiau dėmesio skiriama ir ūgiui. Tai statmena priešinga kampo pusei. Bukojo trikampio aukštis turi savo ypatybes. Jei jis nubrėžtas iš aštrios viršūnės, tada jis patenka ne į šio paprasčiausio daugiakampio šoną, o į jo tęsinį.

Statmenas bisektorius yra linijos atkarpa, kuri išeina iš trikampio paviršiaus centro. Tuo pačiu metu jis yra stačiu kampu.

Darbas su apskritimais

Pradedant mokytis geometrijos, vaikams pakanka suprasti, kaip nupiešti bukukampį trikampį, išmokti jį atskirti nuo kitų tipų ir prisiminti pagrindines jo savybes. Tačiau aukštųjų mokyklų studentams šių žinių neužtenka. Pavyzdžiui, per egzaminą dažnai kyla klausimų apie apibrėžtus ir užrašytus apskritimus. Pirmasis iš jų liečia visas tris trikampio viršūnes, o antrasis turi vieną bendrą tašką su visomis kraštinėmis.

Jau daug sunkiau pastatyti nubrėžtą ar apibrėžtą bukojo kampo trikampį, nes tam pirmiausia reikia išsiaiškinti, kur turi būti apskritimo centras ir jo spindulys. Beje, tokiu atveju būtinu įrankiu taps ne tik pieštukas su liniuote, bet ir kompasas.

Tie patys sunkumai iškyla statant įbrėžtus daugiakampius su trimis kraštinėmis. Matematikai sukūrė įvairias formules, kurios leidžia kuo tiksliau nustatyti jų buvimo vietą.

Įrašyti trikampiai

Kaip minėta anksčiau, jei apskritimas eina per visas tris viršūnes, tai vadinama apibrėžtuoju apskritimu. Pagrindinė jo savybė yra ta, kad ji yra vienintelė. Norint išsiaiškinti, kaip turėtų būti išdėstytas bukojo trikampio apskritimas, reikia atsiminti, kad jo centras yra trijų vidurinių statmenų, einančių į figūros šonus, sankirtoje. Jei smailaus kampo daugiakampyje su trimis viršūnėmis šis taškas bus jo viduje, tai bukukampiame - už jo ribų.

Pavyzdžiui, žinant, kad buku kampo trikampio viena iš kraštinių yra lygi jo spinduliui, galima rasti kampą, esantį priešais žinomą paviršių. Jo sinusas bus lygus rezultatui, padalijus žinomos kraštinės ilgį iš 2R (kur R yra apskritimo spindulys). Tai reiškia, kad kampo nuodėmė bus lygi ½. Taigi kampas bus 150 o.

Jei reikia rasti bukukampio trikampio apibrėžtojo apskritimo spindulį, tai reikės informacijos apie jo kraštinių ilgį (c, v, b) ir plotą S. Juk spindulys skaičiuojamas taip : (cxvxb): 4 x S. Beje, nesvarbu, kokią figūrą turite: universalų bukas trikampis, lygiašonis, dešinysis ar smailus. Bet kurioje situacijoje aukščiau pateiktos formulės dėka galite sužinoti nurodyto daugiakampio plotą su trimis kraštinėmis.

Apriboti trikampiai

Taip pat gana įprasta dirbti su užrašytais apskritimais. Pagal vieną iš formulių tokios figūros spindulys, padaugintas iš ½ perimetro, bus lygus trikampio plotui. Tiesa, norint tai išsiaiškinti, reikia žinoti bukojo trikampio kraštines. Iš tiesų, norint nustatyti ½ perimetro, reikia pridėti jų ilgius ir padalyti iš 2.

Norint suprasti, kur turi būti į bukąjį trikampį įbrėžto apskritimo centras, reikia nubrėžti tris pusiausvyras. Tai linijos, dalijančios kampus. Būtent jų sankirtoje bus apskritimo centras. Tokiu atveju jis bus vienodu atstumu nuo kiekvienos pusės.

Tokio apskritimo, įbrėžto į bukąjį trikampį, spindulys lygus daliniui (p-c) x (p-v) x (p-b): p. Be to, p yra trikampio pusė perimetro, c, v, b yra jo kraštinės.