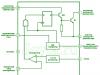
Om vi placerar en singel nummercirkel på koordinatplanet, då är det för dess punkter möjligt att hitta koordinater. Den numeriska cirkeln är placerad så att dess centrum sammanfaller med planets origo, dvs punkten O (0; 0).
Vanligtvis, på en enhetsnummercirkel, markeras punkter som motsvarar origo på cirkeln
- fjärdedelar - 0 eller 2π, π/2, π, (2π)/3,
- mellankvarter - π/4, (3π)/4, (5π)/4, (7π)/4,
- tredje kvartalet - π/6, π/3, (2π)/3, (5π)/6, (7π)/6, (4π)/3, (5π)/3, (11π)/6.
På koordinatplanet, med ovanstående arrangemang av enhetscirkeln på det, kan man hitta koordinaterna som motsvarar dessa punkter i cirkeln.
Det är mycket lätt att hitta koordinaterna för ändarna av kvarteren. Vid punkt 0 i cirkeln är x-koordinaten 1, och y är 0. Vi kan skriva A (0) = A (1; 0).
Slutet av första kvartalet kommer att ligga på den positiva y-axeln. Därför är B (π/2) = B (0; 1).
Slutet av andra kvartalet är på den negativa abskissan: C (π) = C (-1; 0).
Slutet av tredje kvartalet: D ((2π)/3) = D (0; -1).
Men hur hittar man koordinaterna för mittpunkterna i kvartalen? För att göra detta, bygg en rätvinklig triangel. Dess hypotenusa är ett segment från cirkelns mittpunkt (eller origo) till mittpunkten av kvartscirkeln. Detta är cirkelns radie. Eftersom cirkeln är enhet är hypotenusan lika med 1. Därefter dras en vinkelrät från en punkt på cirkeln till valfri axel. Låt det vara till x-axeln. Det visar sig en rätvinklig triangel, vars längder på benen är x- och y-koordinaterna för cirkelns punkt.
En kvartscirkel är 90º. Och en halv fjärdedel är 45º. Eftersom hypotenusan dras till mitten av kvarten, är vinkeln mellan hypotenusan och benet som kommer ut ur origo 45º. Men summan av vinklarna för en triangel är 180º. Därför förblir vinkeln mellan hypotenusan och det andra benet också 45º. Det visar sig vara en likbent rätvinklig triangel.
Från Pythagoras sats får vi ekvationen x 2 + y 2 = 1 2 . Eftersom x = y och 1 2 = 1 förenklas ekvationen till x 2 + x 2 = 1. Löser vi det får vi x = √1 = 1/√2 = √2/2.
Koordinaterna för punkten M 1 (π/4) = M 1 (√2/2; √2/2).
I koordinaterna för punkterna för mittpunkterna i andra kvartal kommer bara tecknen att ändras, och värdemodulerna kommer att förbli desamma, eftersom den rätvinkliga triangeln bara kommer att vända. Vi får:
M2 ((3π)/4) = M2 (-√2/2; √2/2)
M3 ((5π)/4) = M3 (-√2/2; -√2/2)
M4 ((7π)/4) = M4 (√2/2; -√2/2)
Vid bestämning av koordinaterna för de tredje delarna av cirkelns fjärdedelar byggs också en rätvinklig triangel. Om vi tar punkten π/6 och ritar en vinkelrät mot x-axeln, så blir vinkeln mellan hypotenusan och benet som ligger på x-axeln 30º. Det är känt att benet som ligger mitt emot en vinkel på 30º är lika med halva hypotenusan. Så vi har hittat y-koordinaten, den är lika med ½.
Genom att känna till längden på hypotenusan och ett av benen, genom Pythagoras sats finner vi det andra benet:
x 2 + (½) 2 = 1 2
x 2 \u003d 1 - ¼ \u003d ¾
x = √3/2
Således Ti (π/6) = Ti (√3/2; ½).
För punkten för den andra tredjedelen av första kvartalet (π / 3) är det bättre att rita en vinkelrät mot axeln till y-axeln. Då blir vinkeln vid utgången också 30º. Här kommer x-koordinaten redan att vara lika med ½ respektive y √3/2: T 2 (π/3) = T 2 (½; √3/2).
För andra tredje kvartalspoäng kommer tecknen och ordningen på koordinatvärdena att ändras. Alla punkter som är närmare x-axeln kommer att ha ett modulovärde för x-koordinaten lika med √3/2. De punkter som är närmare y-axeln kommer att ha ett modulo y-värde lika med √3/2.
T 3 ((2π)/3) = T 3 (-½; √3/2)
T 4 ((5π)/6) = T 4 (-√3/2; ½)
T 5 ((7π)/6) = T 5 (-√3/2; -½)
T 6 ((4π)/3) = T 6 (-½; -√3/2)
T 7 ((5π)/3) = T 7 (½; -√3/2)
T 8 ((11π)/6) = T 8 (√3/2; -½)
Att tycka om förhandsvisning presentationer skapa ett konto ( konto) Google och logga in: https://accounts.google.com
Bildtexter:
Talcirkel i koordinatplanet
Låt oss upprepa: Enhetscirkeln är en numerisk cirkel, vars radie är lika med 1. R=1 C=2 π + - y x
Om punkten M i den numeriska cirkeln motsvarar talet t, så motsvarar den också talet på formen t+2 π k , där k är vilket heltal som helst (k ϵ Z) . M(t) = M(t+2 π k), där k ϵ Z
Grundläggande layouter Första layout 0 π y x Andra layout y x
x y 1 A(1, 0) B (0, 1) C (- 1, 0) D (0, -1) 0 x>0 y>0 x 0 x 0 y
Hitta koordinaterna för punkten M som motsvarar punkten. 1) 2) x y M P 45° O A
Koordinater för huvudpunkterna i den första layouten 0 2 x 1 0 -1 0 1 y 0 1 0 -1 0 0 x 1 0 -1 0 1 y 0 1 0 -1 0 D y x
MP x y O A Hitta koordinaterna för punkten M som motsvarar punkten. 1) 2) 30°
M P Hitta koordinaterna för punkten M som motsvarar punkten. 1) 2) 30° x y O A B
Med hjälp av symmetriegenskapen hittar vi koordinaterna för punkter som är multipler av y x
Koordinater för huvudpunkterna i den andra layouten x y x y y x
Exempel Hitta koordinaterna för en punkt på en talcirkel. Lösning: P y x
Exempel Hitta punkter med ordinata på en talcirkel Lösning: y x x y x y
Övningar: Hitta koordinaterna för punkterna i den numeriska cirkeln: a) , b) . Hitta punkter med en abskissa på talcirkeln.
Nyckelpunkters koordinater 0 2 x 1 0 -1 0 1 y 0 1 0 -1 0 0 x 1 0 -1 0 1 y 0 1 0 -1 0 Nyckelpunkters koordinater för den första layouten x y x y Nyckelpunkters koordinater för den andra layouten
På ämnet: metodologisk utveckling, presentationer och anteckningar
Didaktiskt material om algebra och början av analys i årskurs 10 (profilnivå) "Siffercirkel på koordinatplanet"
Alternativ 1.1. Hitta en punkt på talcirkeln: A) -2∏ / 3B) 72. Vilken fjärdedel av talcirkeln tillhör punkten 16.3. Hitta vilken ...
Nummercirkelär en enhetscirkel vars punkter motsvarar vissa reella tal.
En enhetscirkel är en cirkel med radie 1.
Allmän bild av talcirkeln.
1) Dess radie tas som en måttenhet.
2) De horisontella och vertikala diametrarna delar upp den numeriska cirkeln i fyra fjärdedelar (se figur). De kallas för första, andra, tredje respektive fjärde kvartalet.
3) Den horisontella diametern betecknas AC, där A är punkten längst till höger.
Den vertikala diametern betecknas BD, där B är den högsta punkten.
Respektive:
första kvartalet är bågen AB
andra kvartalet - båge f.Kr
tredje kvartalet - båge CD
fjärde kvartalet - båge DA
4) Startpunkten för den numeriska cirkeln är punkt A.
Talcirkeln kan räknas antingen medurs eller moturs.
Räkna från punkt A moturs kallas positiv riktning.
Att räkna från punkt A medurs kallas negativ riktning.
Nummercirkel på koordinatplanet.
Centrum av radien för den numeriska cirkeln motsvarar origo (nummer 0).
Horisontell diameter motsvarar axeln x, vertikala - axlar y.
Startpunkten A för talcirkeln är på axeln x och har koordinater (1; 0).
Värderingarx ochy i fjärdedelar av en numerisk cirkel:
Huvudvärdena i den numeriska cirkeln:
Namn och platser för huvudpunkterna i talcirkeln:

Hur man kommer ihåg namnen på nummercirkeln.
Det finns några enkla mönster som hjälper dig att enkelt komma ihåg de grundläggande namnen på talcirkeln.
Innan vi börjar minns vi: nedräkningen är i positiv riktning, det vill säga från punkt A (2π) moturs.
1) Låt oss börja med extrema punkter på koordinataxlarna.
Startpunkten är 2π (punkten längst till höger på axeln X lika med 1).
Som ni vet är 2π omkretsen av en cirkel. Så hälften av cirkeln är 1π eller π. Axel X delar cirkeln på mitten. Följaktligen punkten längst till vänster på axeln X lika med -1 kallas π.
Högsta punkten på axeln på, lika med 1, halverar den övre halvcirkeln. Så om halvcirkeln är π, så är halva halvcirkeln π/2.
Samtidigt är π/2 också en fjärdedels cirkel. Vi räknar tre sådana fjärdedelar från den första till den tredje - och vi kommer till den lägsta punkten på axeln på lika med -1. Men om den innehåller tre fjärdedelar, är dess namn 3π/2.

2) Låt oss nu gå vidare till resten av punkterna. Observera: alla motsatta punkter har samma täljare - dessutom är dessa motsatta punkter och i förhållande till axeln på, och i förhållande till axlarnas centrum och i förhållande till axeln X. Detta kommer att hjälpa oss att känna till deras poängvärden utan att fylla på.
Det är nödvändigt att komma ihåg endast värdet på punkterna i det första kvartalet: π / 6, π / 4 och π / 3. Och sedan kommer vi att "se" några mönster:
- Om y-axeln vid punkterna i det andra kvartalet, i motsats till punkterna i det första kvartalet, är siffrorna i täljarna 1 mindre än nämnarna. Ta till exempel punkten π/6. Den motsatta punkten om axeln på har också 6 i nämnaren och 5 i täljaren (1 mindre). Det vill säga namnet på denna punkt: 5π/6. Punkten mittemot π/4 har också 4 i nämnaren och 3 i täljaren (1 mindre än 4) - det vill säga detta är punkten 3π/4.
Punkten mittemot π/3 har också 3 i nämnaren och 1 mindre i täljaren: 2π/3.
 - I förhållande till centrum av koordinataxlarna motsatsen är sant: siffrorna i täljarna för motsatta punkter (i tredje kvartalet) med 1 mer värde nämnare. Ta punkten π/6 igen. Punkten mittemot den i förhållande till mitten har också 6 i nämnaren, och i täljaren är talet 1 till - det vill säga det är 7π / 6.
- I förhållande till centrum av koordinataxlarna motsatsen är sant: siffrorna i täljarna för motsatta punkter (i tredje kvartalet) med 1 mer värde nämnare. Ta punkten π/6 igen. Punkten mittemot den i förhållande till mitten har också 6 i nämnaren, och i täljaren är talet 1 till - det vill säga det är 7π / 6.
Punkten mittemot punkten π/4 har också 4 i nämnaren, och talet i täljaren är 1 till: 5π/4.
Punkten mittemot punkten π/3 har också 3 i nämnaren, och talet i täljaren är 1 till: 4π/3.
- Axel relativ X(fjärde kvarten) saken är svårare. Här är det nödvändigt att lägga till värdet av nämnaren ett tal som är mindre än 1 - denna summa kommer att vara lika med den numeriska delen av täljaren för den motsatta punkten. Låt oss börja om med π/6. Låt oss lägga till värdet på nämnaren, lika med 6, ett tal som är 1 mindre än detta tal - det vill säga 5. Vi får: 6 + 5 = 11. Därmed motsatt det med avseende på axeln X punkten kommer att ha 6 i nämnaren och 11 i täljaren, dvs 11π/6.
Punkt π/4. Vi adderar till nämnarens värde ett tal 1 mindre: 4 + 3 = 7. Därmed motsatt det med avseende på axeln X punkten har 4 i nämnaren och 7 i täljaren, det vill säga 7π/4.
Punkt π/3. Nämnaren är 3. Vi adderar till 3 ett tal mindre - det vill säga 2. Vi får 5. Därför har den motsatta punkten 5 i täljaren - och detta är punkten 5π / 3.
3) Ytterligare en regelbundenhet för mittpunkterna i kvartalen. Det är tydligt att deras nämnare är 4. Låt oss vara uppmärksamma på täljarna. Täljaren i mitten av första kvartalet är 1π (men 1 är inte vanligt att skriva). Täljaren för mitten av andra kvartalet är 3π. Täljaren för mitten av tredje kvartalet är 5π. Täljaren för mitten av fjärde kvartalet är 7π. Det visar sig att i täljarna för mittpunkterna i kvartalen finns de fyra första udda talen i stigande ordning:
(1)π, 3π, 5π, 7π.
Det är också väldigt enkelt. Eftersom mittpunkterna i alla fjärdedelar har 4 i nämnaren känner vi dem redan Fullständiga namn: π/4, 3π/4, 5π/4, 7π/4.
Funktioner i talcirkeln. Jämförelse med en tallinje.
Som du vet, på tallinjen, motsvarar varje punkt singularis. Till exempel, om punkt A på en rät linje är lika med 3, kan den inte vara lika med något annat tal.
Det är annorlunda på talcirkeln eftersom det är en cirkel. Till exempel, för att komma från punkt A i cirkeln till punkt M, kan du göra det som på en rät linje (endast efter att ha passerat bågen), eller så kan du gå runt hela cirkeln och sedan komma till punkt M. Slutsats:
Låt punkten M vara lika med något tal t. Som vi vet är en cirkels omkrets 2π. Därför kan vi skriva punkten för cirkeln t på två sätt: t eller t + 2π. Dessa är likvärdiga värden.
Det vill säga t = t + 2π. Den enda skillnaden är att du i det första fallet kom till punkt M omedelbart utan att göra en cirkel, och i det andra fallet gjorde du en cirkel, men hamnade i samma punkt M. Du kan göra två, tre och tvåhundra sådana cirklar.. Om vi betecknar antalet cirklar med bokstaven k, får vi ett nytt uttryck:
t = t + 2π k.
Därav formeln:
Nummercirkelekvation
(den andra ekvationen finns i avsnittet "Sinus, cosinus, tangent, cotangens"):
x2 + y2 = 1 |
Nummercirkelär en enhetscirkel vars punkter motsvarar vissa reella tal.
En enhetscirkel är en cirkel med radie 1.
Allmän bild av talcirkeln.
1) Dess radie tas som en måttenhet.
2) De horisontella och vertikala diametrarna delar upp den numeriska cirkeln i fyra fjärdedelar. De kallas för första, andra, tredje respektive fjärde kvartalet.
3) Den horisontella diametern betecknas AC, där A är den yttersta höger punkt.
Den vertikala diametern betecknas BD, där B är den högsta punkten.
Respektive:
första kvartalet är bågen AB
andra kvartalet - båge f.Kr
tredje kvartalet - arc CD
fjärde kvartalet - båge DA
4) Startpunkten för den numeriska cirkeln är punkt A.
Talcirkeln kan räknas antingen medurs eller moturs.
Räknar från punkt A mot medurs kallas positiv riktning.
Räknar från punkt A på medurs kallas negativ riktning.
Nummercirkel på koordinatplanet.
Centrum av radien för den numeriska cirkeln motsvarar origo (nummer 0).
Horisontell diameter motsvarar axeln x, vertikala - axlar y.
Utgångspunkt En talcirkelti är på axelnxoch har koordinater (1; 0).

Namn och platser för huvudpunkterna i talcirkeln:

Hur man kommer ihåg namnen på nummercirkeln.
Det finns några enkla mönster som hjälper dig att enkelt komma ihåg de grundläggande namnen på talcirkeln.
Innan vi börjar minns vi: nedräkningen är i positiv riktning, det vill säga från punkt A (2π) moturs.

1) Låt oss utgå från ytterpunkterna på koordinataxlarna.
Startpunkten är 2π (punkten längst till höger på axeln X lika med 1).
Som ni vet är 2π omkretsen av en cirkel. Så halva cirkeln är 1π eller π. Axel X delar cirkeln på mitten. Följaktligen punkten längst till vänster på axeln X lika med -1 kallas π.
Högsta punkten på axeln på, lika med 1, halverar den övre halvcirkeln. Så om halvcirkeln är π, så är halva halvcirkeln π/2.
Samtidigt är π/2 också en fjärdedels cirkel. Vi räknar tre sådana fjärdedelar från den första till den tredje - och vi kommer till den lägsta punkten på axeln på lika med -1. Men om den innehåller tre fjärdedelar, är dess namn 3π/2.
2) Låt oss nu gå vidare till resten av punkterna. Observera: alla motsatta punkter har samma nämnare - dessutom är dessa motsatta punkter och i förhållande till axeln på, och i förhållande till axlarnas centrum och i förhållande till axeln X. Detta kommer att hjälpa oss att känna till deras poängvärden utan att fylla på.

Det är nödvändigt att komma ihåg endast värdet på punkterna i det första kvartalet: π / 6, π / 4 och π / 3. Och sedan kommer vi att "se" några mönster:
- Axel relativ på
vid punkterna i det andra kvartalet, i motsats till punkterna i det första kvartalet, är siffrorna i täljarna 1 mindre än nämnarna. Ta till exempel punkten π/6. Den motsatta punkten om axeln på har också 6 i nämnaren och 5 i täljaren (1 mindre). Det vill säga namnet på denna punkt: 5π/6. Punkten mittemot π/4 har också 4 i nämnaren och 3 i täljaren (1 mindre än 4) - det vill säga detta är punkten 3π/4.
Punkten mittemot π/3 har också 3 i nämnaren och 1 mindre i täljaren: 2π/3.
- I förhållande till centrum av koordinataxlarna motsatsen är sant: siffrorna i täljarna för de motsatta punkterna (i tredje kvartalet) är 1 mer än nämnarnas värden. Ta punkten π/6 igen. Punkten mittemot den i förhållande till mitten har också 6 i nämnaren, och i täljaren är talet 1 till - det vill säga det är 7π / 6.
Punkten mittemot punkten π/4 har också 4 i nämnaren, och talet i täljaren är 1 till: 5π/4.
Punkten mittemot punkten π/3 har också 3 i nämnaren, och talet i täljaren är 1 till: 4π/3.
- Axel relativ X(fjärde kvarten) saken är svårare. Här är det nödvändigt att lägga till värdet på nämnaren ett tal som är 1 mindre - denna summa kommer att vara lika med den numeriska delen av täljaren för den motsatta punkten. Låt oss börja om med π/6. Låt oss lägga till värdet på nämnaren, lika med 6, ett tal som är 1 mindre än detta tal - det vill säga 5. Vi får: 6 + 5 = 11. Därmed motsatt det med avseende på axeln X punkten kommer att ha 6 i nämnaren och 11 i täljaren - det vill säga 11π / 6.
Punkt π/4. Vi adderar till nämnarens värde ett tal 1 mindre: 4 + 3 = 7. Därmed motsatt det med avseende på axeln X punkten har 4 i nämnaren och 7 i täljaren, dvs 7π/4.
Punkt π/3. Nämnaren är 3. Vi adderar till 3 ett tal mindre - det vill säga 2. Vi får 5. Därför har den motsatta punkten 5 i täljaren - och detta är punkten 5π / 3.
3) Ytterligare en regelbundenhet för mittpunkterna i kvartalen. Det är tydligt att deras nämnare är 4. Låt oss vara uppmärksamma på täljarna. Täljaren i mitten av första kvartalet är 1π (men 1 är inte vanligt att skriva). Täljaren för mitten av andra kvartalet är 3π. Täljaren för mitten av tredje kvartalet är 5π. Täljaren för mitten av fjärde kvartalet är 7π. Det visar sig att i täljarna för mittpunkterna i kvartalen finns de fyra första udda talen i stigande ordning:
(1)π, 3π, 5π, 7π.
Det är också väldigt enkelt. Eftersom mitten av alla fjärdedelar har 4 i nämnaren känner vi redan till deras fullständiga namn: π/4, 3π/4, 5π/4, 7π/4.
Funktioner i talcirkeln. Jämförelse med en tallinje.
Som du vet, på tallinjen, motsvarar varje punkt ett enda tal. Till exempel, om punkt A på en rät linje är lika med 3, kan den inte vara lika med något annat tal.
Det är annorlunda på talcirkeln eftersom det är en cirkel. Till exempel, för att komma från punkt A i cirkeln till punkt M, kan du göra det som på en rät linje (endast efter att ha passerat bågen), eller så kan du gå runt hela cirkeln och sedan komma till punkt M. Slutsats:
Låt punkten M vara lika med något tal t. Som vi vet är en cirkels omkrets 2π. Därför kan vi skriva punkten för cirkeln t på två sätt: t eller t + 2π. Dessa är likvärdiga värden.
Det vill säga t = t + 2π. Den enda skillnaden är att du i det första fallet kom till punkt M omedelbart utan att göra en cirkel, och i det andra fallet gjorde du en cirkel, men hamnade i samma punkt M. Du kan göra två, tre och tvåhundra sådana cirklar.. Om vi betecknar antalet cirklar med bokstaven n, får vi ett nytt uttryck:
t = t + 2π n.
Därav formeln:

Mycket tid ägnas åt talcirkeln i årskurs 10. Detta beror på betydelsen av detta matematiska objekt för hela matematikkursen.
Rätt val av läromedel är av stor betydelse för en god assimilering av materialet. Videohandledningar är bland de mest effektiva av dessa verktyg. PÅ senare tid de når toppen av popularitet. Därför släpade författaren inte efter nuet och utvecklade en sådan underbar manual för att hjälpa matematiklärare - en videolektion om ämnet "Nummercirkel på koordinatplanet".
Den här lektionen är 15:22 minuter lång. Detta är praktiskt taget den maximala tid som en lärare kan lägga på en oberoende förklaring av materialet om ämnet. Eftersom det tar så mycket tid att förklara nytt material är det nödvändigt att välja de mest effektiva uppgifterna och övningarna för konsolidering, samt lyfta fram ytterligare en lektion där eleverna ska lösa uppgifter om detta ämne.
Lektionen börjar med bilden av en numerisk cirkel i ett koordinatsystem. Författaren bygger denna cirkel och förklarar sina handlingar. Sedan namnger författaren skärningspunkterna för den numeriska cirkeln med koordinataxlarna. Följande förklarar vilka koordinater cirkelns punkter kommer att ha i olika håll.
Efter det minns författaren hur cirkelekvationen ser ut. Och lyssnarnas uppmärksamhet presenteras för två layouter med bilden av några punkter på cirkeln. På grund av detta visar författaren i nästa steg hur koordinaterna för cirkeln pekar motsvara vissa siffror markerade på mallarna. Detta resulterar i en värdetabell för variablerna x och y i cirkelekvationen.
Vidare föreslås det att överväga ett exempel där det är nödvändigt att bestämma koordinaterna för cirkelns punkter. Innan man börjar lösa exemplet införs en anmärkning som hjälper till att lösa. Och så dyker en komplett, tydligt strukturerad och illustrerad lösning upp på skärmen. Det finns också tabeller som gör det lättare att förstå kärnan i exemplet.
Sedan övervägs ytterligare sex exempel, som är mindre tidskrävande än det första, men inte mindre viktiga och reflekterar huvudtanken lektion. Här presenteras lösningarna i till fullo, med en detaljerad berättelse och med visuella inslag. Lösningen innehåller nämligen ritningar som illustrerar lösningens förlopp, och en matematisk notation som bildar elevernas matematiska läskunnighet.
Läraren kan begränsa sig till de exempel som tas upp i lektionen, men det kanske inte räcker för en kvalitativ assimilering av materialet. Därför är det helt enkelt extremt viktigt att välja uppgifter att konsolidera.

Lektionen kan vara användbar inte bara för lärare, vars tid ständigt är begränsad, utan också för elever. Speciellt för dem som får en familjeutbildning eller ägnar sig åt egenutbildning. Materialet kan användas av de elever som missade lektionen om detta ämne.
TEXTTOLKNING:
Ämnet för vår lektion är "NUMERISK CIRKEL PÅ KOORDINATPLANET"
Vi är redan bekanta med det kartesiska rektangulära koordinatsystemet xOy (x o y). I detta koordinatsystem kommer vi att ordna talcirkeln så att cirkelns mittpunkt är i linje med origo och dess radie kommer att tas som skalsegment.
Startpunkten A för den numeriska cirkeln är i linje med punkten med koordinaterna (1; 0), B - med punkten (0; 1), C - med (-1; 0) (minus ett, noll) och D - med (0; - 1)(noll, minus ett).
(se bild 1)
Eftersom varje punkt i den numeriska cirkeln har sina egna koordinater i xOy-systemet (x om y), så är för punkterna i den första fjärdedelen ikx större än noll och y är större än noll;
Andra kvartalet ich mindre än noll och y är större än noll,
för punkter i tredje kvartalet är uh mindre än noll och y är mindre än noll,
och för fjärde kvartalet är uh större än noll och y är mindre än noll
För varje punkt E (x; y) (med koordinaterna x, y) i den numeriska cirkeln, är olikheterna -1≤ x≤ 1, -1≤y≤1 (x är större än eller lika med minus ett, men mindre än eller lika med ett; y är större än eller är lika med minus ett, men mindre än eller lika med ett).
Kom ihåg att ekvationen för en cirkel med radien R centrerad vid origo är x 2 + y 2 = R 2 (x i kvadrat plus y i kvadrat är lika med er i kvadrat). Och för enhetscirkeln R \u003d 1, så får vi x 2 + y 2 \u003d 1
(x i kvadrat plus y i kvadrat är lika med ett).
Låt oss hitta koordinaterna för punkterna i den numeriska cirkeln, som presenteras på två layouter (se fig. 2, 3)
Låt punkt E, som motsvarar
(pi gånger fyra) - mitten av den första fjärdedelen som visas i figuren. Från punkten E släpper vi den vinkelräta EK till linjen OA och betraktar triangeln OEK. Vinkel AOE =45 0, eftersom bågen AE är hälften av bågen AB. Därför är triangeln OEK en likbent rätvinklig, där OK = EK. Därför är abskissan och ordinatan för punkten E lika, dvs. x är lika med y. För att hitta koordinaterna för punkt E löser vi ekvationssystemet: (x är lika med y - systemets första ekvation och x kvadrat plus y kvadrat är lika med ett - systemets andra ekvation) I den andra ekvationen systemets ekvation, istället för x, vi ersätter y, vi får 2y 2 \u003d 1 (två y kvadrat är lika med en), varav y \u003d (y = en dividerad med roten av två är lika med roten av två dividerat med två) (ordinatan är positiv) Detta betyder att punkten E i det rektangulära koordinatsystemet har koordinater (,) (roten ur två dividerat med två, roten ur två dividerat med två).
Om vi argumenterar på samma sätt hittar vi koordinaterna för punkterna som motsvarar andra nummer i den första layouten och get: motsvarar en punkt med koordinater (- ,) (minus roten av två dividerat med två, roten av två delat med två); för - (-,-) (minus roten av två dividerat med två, minus roten av två dividerat med två); för (sju pi gånger fyra) (,) (roten av två delat med två, minus kvadratroten av två delat med två).
Låt punkt D motsvara (fig. 5). Låt oss släppa vinkelrät från DP(de pe) till OA och betrakta triangeln ODP. Hypotenusan för denna triangel OD är lika med radien för enhetscirkeln, det vill säga en, och vinkeln DOP är lika med trettio grader, eftersom bågen AD \u003d digi AB (en de är lika med en tredjedel av en be) ), och bågen AB är nittio grader. Därför är DP \u003d (de pe är lika med en sekund O de är lika med en sekund) Eftersom benet mitt emot vinkeln på trettio grader är lika med halva hypotenusan, det vill säga y \u003d (y är lika med en sekund ). Genom att tillämpa Pythagoras sats får vi OR 2 \u003d OD 2 - DP 2 (o pe kvadrat är lika med o de square minus de pe square), men OR \u003d x (o pe är lika med x). Så x 2 \u003d OD 2 - DP 2 \u003d
så x 2 \u003d (x i kvadrat är lika med tre fjärdedelar) och x \u003d (x är lika med roten av tre och två).
X är positivt, eftersom är under första kvartalet. Vi fick att punkt D i ett rektangulärt koordinatsystem har koordinater (,) roten av tre dividerat med två, en sekund.
Genom att argumentera på ett liknande sätt hittar vi koordinaterna för punkterna som motsvarar andra nummer i den andra layouten och skriver alla data som erhålls i tabellerna:
Tänk på exempel.
EXEMPEL 1. Hitta koordinaterna för punkterna i den numeriska cirkeln: a) C 1 ();
b) C2(); c) C3 (41n); d) C4 (-26n). (tse ett motsvarar trettiofem pi gånger fyra, tse två motsvarar minus fyrtionio pi till tre, tse tre motsvarar fyrtioen pi, tse fyra motsvarar minus tjugosex pi).
Lösning. Låt oss använda påståendet som erhölls tidigare: om punkten D i den numeriska cirkeln motsvarar talet t, så motsvarar den också valfritt tal av formen t + 2πk(te plus två toppar), där ka är vilket heltal som helst, dvs. kϵZ (ka tillhör zet).
a) Vi får = ∙ π = (8 +) ∙π = + 2π ∙ 4. (trettiofem pi gånger fyra är trettiofem gånger fyra, multiplicerat med pi är lika med summan av åtta och tre fjärdedelar, multiplicerat med pi är lika med tre pi gånger fyra plus produkten av två pi gånger fyra. Det betyder att talet trettiofem pi gånger fyra motsvarar samma punkt på den numeriska cirkeln som talet tre pi gånger fyra. Med tabell 1 får vi С 1 () = С 1 (-;) .
b) På liknande sätt, koordinaterna С 2: = ∙ π = - (16 + ∙π = + 2π ∙ (- 8). Därav talet
motsvarar samma punkt i talcirkeln som talet. Och talet motsvarar på talcirkeln samma punkt som numret
(visa den andra layouten och tabell 2). För en punkt har vi x = , y =.
c) 41π \u003d 40π + π \u003d π + 2π ∙ 20. Därför motsvarar talet 41π samma punkt i den numeriska cirkeln som talet π - detta är en punkt med koordinater (-1; 0).
d) - 26π \u003d 0 + 2π ∙ (- 13), det vill säga talet - 26π motsvarar samma punkt i den numeriska cirkeln som talet noll, detta är punkten med koordinater (1; 0).

EXEMPEL 2. Hitta punkter på talcirkeln med ordinatan y \u003d
Lösning. Linjen y = skär talcirkeln i två punkter. En punkt motsvarar ett nummer, den andra punkten motsvarar ett nummer,
Därför erhålls alla poäng genom att addera ett helt varv 2πk där k visar hur mycket hela varv gör en poäng, dvs. vi får
och för valfritt tal alla tal på formen + 2πk. Ofta säger de i sådana fall att de har fått två serier av värden: + 2πk, + 2πk.
EXEMPEL 3. Hitta punkter på talcirkeln med abskissan x = och skriv ner vilka tal t de motsvarar.
Lösning. Hetero X= skär talcirkeln i två punkter. En punkt motsvarar ett nummer (se andra layouten),
och därav valfritt tal av formen + 2πk. Och den andra punkten motsvarar ett tal, och därmed ett valfritt tal av formen + 2πk. Dessa två serier av värden kan täckas i en post: ± + 2πk (plus minus två pi med tre plus två pi).
EXEMPEL 4. Hitta punkter med en ordinata på en talcirkel på> och skriv ner vilka siffror de motsvarar.
Linjen y \u003d skär talcirkeln i två punkter M och P. Och olikheten y\u003e motsvarar punkterna för den öppna bågen MP, detta betyder bågar utan ändar (det vill säga utan och), när man rör sig runt cirkeln moturs, med början från punkten M och slutar vid punkten P. Därför är kärnan i den analytiska representationen av bågen MP olikheten< t < (тэ больше, чем пи на три, но меньше двух пи на три) , а сама аналитическая запись дуги имеет вид + 2πk < t < + 2πk(тэ больше, чем пи на три плюс два пи ка, но меньше двух пи на три плюс два пи ка).
EXEMPEL 5. Hitta punkter med ordinata på en talcirkel på < и записать, каким числам t они соответствуют.
Linjen y \u003d skär talcirkeln i två punkter M och P. Och olikheten y< соответствуют точки открытой дуги РМ при движении по окружности против часовой стрелки, начиная с точки Р, а заканчивая в точке М. Значит, ядром аналитической записи дуги РМ является неравенство < t < (тэ больше, чем минус четыре пи на три, но меньше пи на три) , а сама аналитическая запись дуги имеет вид
2πk< t < + 2πk (тэ больше, чем минус четыре пи на три плюс два пи ка, но меньше пи на три плюс два пи ка).
EXEMPEL 6. Hitta punkter med en abskissa på en talcirkel X> och skriv ner vilka siffror de motsvarar.
Den räta linjen x = skär den numeriska cirkeln i två punkter M och P. Olikheten x > motsvarar punkterna i den öppna bågen PM när man rör sig längs cirkeln moturs med början i punkten P, vilket motsvarar, och slutet kl. punkten M, som motsvarar. Därför är kärnan i den analytiska notationen för bågen PM ojämlikheten< t <
(te är större än minus två pi gånger tre, men mindre än två pi gånger tre), och den analytiska notationen för själva bågen har formen + 2πk< t < + 2πk (тэ больше, чем минус два пи на три плюс два пи ка, но меньше двух пи на три плюс два пи ка).

EXEMPEL 7. Hitta punkter med en abskissa på en talcirkel X < и записать, каким числам t они соответствуют.
Linjen x = skär talcirkeln i två punkter M och P. Olikhet x< соответствуют точки открытой дуги МР при движении по окружности против часовой стрелки с началом в точке М, которая соответствует, и концом в точке Р, которая соответствует. Значит, ядром аналитической записи дуги МР является неравенство < t <
(te är mer än två pi gånger tre, men mindre än fyra pi gånger tre), och den analytiska notationen för själva bågen har formen + 2πk< t < + 2πk (тэ больше, чем два пи на три плюс два пи ка, но меньше четырех пи на три плюс два пи ка).