A की गणना निम्नलिखित नियमों के अनुसार की जाती है:

संक्षिप्तता के लिए, संकेतन का उपयोग किया जाता है |ए|. तो, |10| = 10; - 1 / 3 = | 1 / 3 |; | -100| =100, आदि.

हर आकार एक्सकाफी सटीक मान से मेल खाता है | एक्स|. और उसका अर्थ यह निकलता है पहचान पर= |एक्स| सेट परकुछ की तरह तर्क समारोह एक्स.

अनुसूचीयह कार्यनीचे प्रस्तुत है.

के लिए एक्स > 0 |एक्स| = एक्स, और के लिए एक्स< 0 |एक्स|= -एक्स; इस संबंध में, रेखा y = | एक्स| पर एक्स> 0 एक सीधी रेखा के साथ संयुक्त वाई = एक्स(प्रथम निर्देशांक कोण का समद्विभाजक), और कब एक्स< 0 - с прямой y = -x(दूसरे निर्देशांक कोण का समद्विभाजक)।

अलग समीकरणचिह्न के अंतर्गत अज्ञात शामिल करें मापांक.

ऐसे समीकरणों के मनमाने उदाहरण - | एक्स— 1| = 2, |6 — 2एक्स| =3एक्स+1, आदि।

समीकरण हल करनामापांक चिह्न के अंतर्गत अज्ञात को समाहित करना इस तथ्य पर आधारित है कि यदि किसी अज्ञात संख्या x का निरपेक्ष मान एक धनात्मक संख्या a के बराबर है, तो यह संख्या x स्वयं या तो a या -a के बराबर है।

उदाहरण के लिए:, यदि | एक्स| = 10, फिर या एक्स=10, या एक्स = -10.

चलो गौर करते हैं व्यक्तिगत समीकरणों को हल करना.

आइए समीकरण के समाधान का विश्लेषण करें | एक्स- 1| = 2.

आइए मॉड्यूल का विस्तार करेंफिर अंतर एक्स- 1 या तो + 2 या - 2 के बराबर हो सकता है। यदि x - 1 = 2 है, तो एक्स=3; अगर एक्स- 1 = - 2, फिर एक्स= - 1. हम एक प्रतिस्थापन करते हैं और पाते हैं कि ये दोनों मान समीकरण को संतुष्ट करते हैं।

उत्तर।उपरोक्त समीकरण की दो जड़ें हैं: एक्स 1 = 3, एक्स 2 = - 1.

आइए विश्लेषण करें समीकरण का हल | 6 — 2एक्स| = 3एक्स+ 1.

बाद मॉड्यूल विस्तारहमें मिलता है: या 6 - 2 एक्स= 3एक्स+ 1, या 6 - 2 एक्स= - (3एक्स+ 1).

पहले मामले में एक्स= 1, और दूसरे में एक्स= - 7.

इंतिहान।पर एक्स= 1 |6 — 2एक्स| = |4| = 4, 3एक्स+ 1 = 4; यह अदालत से चलता है, एक्स = 1 - जड़दिया गया समीकरण.

पर एक्स = - 7 |6 — 2एक्स| = |20| = 20, 3एक्स+1=-20; चूँकि 20 ≠ -20, तब एक्स= - 7 इस समीकरण का मूल नहीं है.

उत्तर। यूसमीकरण का केवल एक मूल है: एक्स = 1.

इस प्रकार के समीकरण हो सकते हैं हल करें और रेखांकन करें.

तो चलिए निर्णय लेते हैं उदाहरण के लिए, रेखांकन समीकरण | एक्स- 1| = 2.

पहले हम निर्माण करेंगे फ़ंक्शन ग्राफ़िक्स पर = |एक्स- 1|. सबसे पहले, आइए फ़ंक्शन का एक ग्राफ़ बनाएं पर=एक्स- 1:

इसका वह भाग ललित कलाएं, जो अक्ष के ऊपर स्थित है एक्सहम इसे नहीं बदलेंगे. उसके लिए एक्स- 1 > 0 और इसलिए | एक्स-1|=एक्स-1.

ग्राफ़ का वह भाग जो अक्ष के नीचे स्थित होता है एक्स, आइए चित्रित करें संतुलितइस अक्ष के सापेक्ष. क्योंकि इस भाग के लिए एक्स - 1 < 0 и соответственно |एक्स - 1|= - (एक्स - 1). परिणामस्वरूप रेखा(ठोस रेखा) और इच्छा फ़ंक्शन ग्राफ़आप = | एक्स—1|.

यह रेखा आपस में प्रतिच्छेद करेगी सीधा पर= 2 दो बिंदुओं पर: एम 1 एब्सिस्सा -1 के साथ और एम 2 एब्सिस्सा 3 के साथ। और, तदनुसार, समीकरण | एक्स- 1| =2 दो जड़ें होंगी: एक्स 1 = - 1, एक्स 2 = 3.

मॉड्यूल उन चीजों में से एक है जिसके बारे में हर किसी ने सुना है, लेकिन वास्तव में कोई भी वास्तव में नहीं समझता है। इसलिए, आज मॉड्यूल के साथ समीकरणों को हल करने के लिए समर्पित एक बड़ा पाठ होगा।

मैं तुरंत कहूंगा: पाठ कठिन नहीं होगा। और सामान्य तौर पर, मॉड्यूल एक अपेक्षाकृत सरल विषय है। “हाँ, बिल्कुल, यह जटिल नहीं है! यह मुझे हैरत में डाल देता है!" - कई छात्र कहेंगे, लेकिन ये सभी दिमागी दरारें इस तथ्य के कारण होती हैं कि ज्यादातर लोगों के दिमाग में ज्ञान नहीं, बल्कि किसी तरह की बकवास होती है। और इस पाठ का लक्ष्य बकवास को ज्ञान में बदलना है :)

थोड़ा सिद्धांत

तो चलते हैं। आइए सबसे महत्वपूर्ण बात से शुरू करें: मॉड्यूल क्या है? मैं आपको याद दिला दूं कि किसी संख्या का मापांक बिल्कुल वही संख्या होता है, लेकिन ऋण चिह्न के बिना लिया जाता है। उदाहरण के लिए, $\left| -5 \दाएं|=5$. या $\left| -129.5 \दाएँ|=$129.5.

क्या यह इतना आसान है? हाँ, सरल. तो फिर किसी धनात्मक संख्या का निरपेक्ष मान क्या है? यहां यह और भी सरल है: एक धनात्मक संख्या का मापांक स्वयं इस संख्या के बराबर होता है: $\left| 5 \दाएं|=5$; $\बाएं| 129.5 \right|=$129.5, आदि।

यह एक जिज्ञासु बात निकली: अलग-अलग नंबरएक ही मॉड्यूल हो सकता है. उदाहरण के लिए: $\left| -5 \दाएँ|=\बाएँ| 5 \दाएं|=5$; $\बाएं| -129.5 \दाएं|=\बाएं| 129.5\दाएं|=$129.5. यह देखना आसान है कि ये किस प्रकार की संख्याएँ हैं जिनका मॉड्यूल समान है: ये संख्याएँ विपरीत हैं। इस प्रकार, हम स्वयं ध्यान दें कि विपरीत संख्याओं के मॉड्यूल बराबर हैं:

\[\बाएं| -ए \दाएं|=\बाएं| ए\दाएं|\]

एक और महत्वपूर्ण तथ्य: मापांक कभी ऋणात्मक नहीं होता. हम जो भी संख्या लेते हैं - चाहे वह सकारात्मक हो या नकारात्मक - उसका मापांक हमेशा सकारात्मक (या, चरम मामलों में, शून्य) निकलता है। इसीलिए मापांक को अक्सर किसी संख्या का निरपेक्ष मान कहा जाता है।

इसके अलावा, यदि हम धनात्मक और ऋणात्मक संख्या के लिए मापांक की परिभाषा को जोड़ते हैं, तो हमें सभी संख्याओं के लिए मापांक की एक वैश्विक परिभाषा प्राप्त होती है। अर्थात्: यदि संख्या धनात्मक (या शून्य) है तो किसी संख्या का मापांक स्वयं संख्या के बराबर होता है, या यदि संख्या ऋणात्मक है तो विपरीत संख्या के बराबर होता है। आप इसे सूत्र के रूप में लिख सकते हैं:

शून्य का भी एक मापांक होता है, लेकिन वह सदैव शून्य के बराबर होता है। इसके अलावा शून्य एकवचन, जिसका कोई विपरीत नहीं है।

इस प्रकार, यदि हम फ़ंक्शन $y=\left| पर विचार करते हैं x \right|$ और इसका ग्राफ़ बनाने का प्रयास करें, आपको कुछ इस तरह मिलेगा:

मापांक ग्राफ़ और समीकरण को हल करने का उदाहरण

इस चित्र से यह तुरंत स्पष्ट है कि $\left| -एम \दाएं|=\बाएं| m \right|$, और मापांक ग्राफ कभी भी x-अक्ष से नीचे नहीं आता है। लेकिन इतना ही नहीं: लाल रेखा सीधी रेखा $y=a$ को चिह्नित करती है, जो सकारात्मक $a$ के लिए, हमें एक साथ दो मूल देती है: $((x)_(1))$ और $((x) _(2)) $, लेकिन हम इसके बारे में बाद में बात करेंगे :)

विशुद्ध रूप से बीजगणितीय परिभाषा के अलावा, एक ज्यामितीय परिभाषा भी है। मान लीजिए कि संख्या रेखा पर दो बिंदु हैं: $((x)_(1))$ और $((x)_(2))$। इस मामले में, अभिव्यक्ति $\left| ((x)_(1))-((x)_(2)) \right|$ केवल निर्दिष्ट बिंदुओं के बीच की दूरी है। या, यदि आप चाहें, तो इन बिंदुओं को जोड़ने वाले खंड की लंबाई:

मापांक एक संख्या रेखा पर बिंदुओं के बीच की दूरी है

इस परिभाषा का यह भी तात्पर्य है कि मापांक हमेशा गैर-नकारात्मक होता है। लेकिन पर्याप्त परिभाषाएँ और सिद्धांत - आइए वास्तविक समीकरणों पर चलते हैं :)

मूल सूत्र

ठीक है, हमने परिभाषा सुलझा ली है। लेकिन इससे यह आसान नहीं हुआ। इसी मॉड्यूल वाले समीकरणों को कैसे हल करें?

शांत, बिल्कुल शांत. आइए सबसे सरल चीज़ों से शुरुआत करें। कुछ इस तरह विचार करें:

\[\बाएं| x\दाएं|=3\]

तो $x$ का मापांक 3 है। $x$ किसके बराबर हो सकता है? खैर, परिभाषा को देखते हुए, हम $x=3$ से काफी खुश हैं। वास्तव में:

\[\बाएं| 3\दाएं|=3\]

क्या अन्य संख्याएँ हैं? ऐसा प्रतीत होता है कि कैप संकेत दे रहा है कि वहाँ है। उदाहरण के लिए, $x=-3$ भी $\left| है -3 \दाएं|=3$, अर्थात्। आवश्यक समानता संतुष्ट है.

तो शायद अगर हम खोजें और सोचें, तो हमें और भी संख्याएँ मिलेंगी? लेकिन इसे तोड़ दो: अधिक संख्यानहीं। समीकरण $\बाएँ| x \right|=3$ के केवल दो मूल हैं: $x=3$ और $x=-3$।

अब कार्य को थोड़ा जटिल बनाते हैं। फ़ंक्शन $f\left(x \right)$ को वेरिएबल $x$ के बजाय मापांक चिह्न के नीचे लटकने दें, और दाईं ओर ट्रिपल के स्थान पर एक मनमाना संख्या $a$ डालें। हमें समीकरण मिलता है:

\[\बाएं| f\left(x \right) \right|=a\]

तो हम इसे कैसे हल कर सकते हैं? मैं आपको याद दिला दूं: $f\left(x \right)$ एक मनमाना फ़ंक्शन है, $a$ कोई भी संख्या है। वे। और कुछ भी! उदाहरण के लिए:

\[\बाएं| 2x+1 \दाएं|=5\]

\[\बाएं| 10x-5 \दाएं|=-65\]

आइए दूसरे समीकरण पर ध्यान दें. आप उसके बारे में तुरंत कह सकते हैं: उसकी कोई जड़ें नहीं हैं। क्यों? यह सही है: क्योंकि इसके लिए आवश्यक है कि मापांक बराबर हो ऋणात्मक संख्या, जो कभी नहीं होता है, क्योंकि हम पहले से ही जानते हैं कि मापांक हमेशा एक सकारात्मक संख्या या चरम मामलों में शून्य होता है।

लेकिन पहले समीकरण के साथ सब कुछ अधिक मज़ेदार है। दो विकल्प हैं: या तो मापांक चिह्न के नीचे एक सकारात्मक अभिव्यक्ति है, और फिर $\left| 2x+1 \right|=2x+1$, या यह अभिव्यक्ति अभी भी नकारात्मक है, और फिर $\left| 2x+1 \right|=-\left(2x+1 \right)=-2x-1$. पहले मामले में, हमारा समीकरण इस प्रकार फिर से लिखा जाएगा:

\[\बाएं| 2x+1 \दाएं|=5\दायां तीर 2x+1=5\]

और अचानक यह पता चलता है कि सबमॉड्यूलर अभिव्यक्ति $2x+1$ वास्तव में सकारात्मक है - यह संख्या 5 के बराबर है। हम इस समीकरण को सुरक्षित रूप से हल कर सकते हैं - परिणामी मूल उत्तर का एक भाग होगा:

जो लोग विशेष रूप से अविश्वासी हैं वे मूल समीकरण में पाए गए मूल को प्रतिस्थापित करने का प्रयास कर सकते हैं और सुनिश्चित कर सकते हैं कि मापांक के तहत वास्तव में एक सकारात्मक संख्या है।

आइए अब एक नकारात्मक सबमॉड्यूलर अभिव्यक्ति के मामले को देखें:

\[\बाएं\( \शुरू(संरेखित)& \बाएं| 2x+1 \दाएं|=5 \\& 2x+1 \lt 0 \\\end(संरेखित) \दाएं.\दायां तीर -2x-1=5 \दायाँ तीर 2x+1=-5\]

उफ़! फिर, सब कुछ स्पष्ट है: हमने मान लिया कि $2x+1 \lt 0$, और परिणामस्वरूप हमें वह मिला $2x+1=-5$ - वास्तव में, यह अभिव्यक्ति है शून्य से भी कम. हम परिणामी समीकरण को हल करते हैं, जबकि पहले से ही यह जानते हुए कि पाया गया मूल हमारे लिए उपयुक्त होगा:

कुल मिलाकर, हमें फिर से दो उत्तर प्राप्त हुए: $x=2$ और $x=3$। हाँ, गणनाओं की मात्रा अत्यंत सरल समीकरण $\left| से थोड़ी अधिक निकली x \right|=3$, लेकिन बुनियादी तौर पर कुछ भी नहीं बदला है। तो शायद कुछ है सार्वभौमिक एल्गोरिथ्म?

हां, ऐसा एल्गोरिदम मौजूद है। और अब हम इसका विश्लेषण करेंगे.

मापांक चिन्ह से छुटकारा पाना

आइए हमें समीकरण $\left| दिया जाए f\left(x \right) \right|=a$, और $a\ge 0$ (अन्यथा, जैसा कि हम पहले से ही जानते हैं, कोई जड़ें नहीं हैं)। फिर आप निम्नलिखित नियम का उपयोग करके मापांक चिह्न से छुटकारा पा सकते हैं:

\[\बाएं| f\left(x \right) \right|=a\राइटएरो f\left(x \right)=\pm a\]

इस प्रकार, मापांक वाला हमारा समीकरण दो भागों में विभाजित हो जाता है, लेकिन मापांक के बिना। बस इतनी ही है तकनीक! आइए कुछ समीकरणों को हल करने का प्रयास करें। आइए इसी से शुरुआत करें

\[\बाएं| 5x+4 \दाएं|=10\दायां तीर 5x+4=\pm 10\]

आइए दाहिनी ओर दस प्लस होने पर अलग से और माइनस होने पर अलग से विचार करें। हमारे पास है:

\[\begin(संरेखित करें)& 5x+4=10\दायां तीर 5x=6\दायां तीर x=\frac(6)(5)=1,2; \\& 5x+4=-10\दायां तीर 5x=-14\दायां तीर x=-\frac(14)(5)=-2.8. \\\end(संरेखित करें)\]

बस इतना ही! हमें दो मूल मिले: $x=1.2$ और $x=-2.8$। संपूर्ण समाधान में वस्तुतः दो पंक्तियाँ थीं।

ठीक है, कोई सवाल नहीं, आइए कुछ और गंभीर बात पर गौर करें:

\[\बाएं| 7-5x\दाएं|=13\]

फिर से हम मॉड्यूल को प्लस और माइनस के साथ खोलते हैं:

\[\begin(संरेखित करें)& 7-5x=13\दायां तीर -5x=6\दायां तीर x=-\frac(6)(5)=-1,2; \\& 7-5x=-13\राइटएरो -5x=-20\राइटएरो x=4. \\\end(संरेखित करें)\]

कुछ पंक्तियाँ फिर से - और उत्तर तैयार है! जैसा कि मैंने कहा, मॉड्यूल के बारे में कुछ भी जटिल नहीं है। आपको बस कुछ नियम याद रखने होंगे। इसलिए, हम आगे बढ़ते हैं और वास्तव में अधिक जटिल कार्यों से शुरुआत करते हैं।

दायीं ओर के चर का मामला

अब इस समीकरण पर विचार करें:

\[\बाएं| 3x-2 \दाएं|=2x\]

यह समीकरण पिछले सभी समीकरणों से मौलिक रूप से भिन्न है। कैसे? और तथ्य यह है कि समान चिह्न के दाईं ओर अभिव्यक्ति $2x$ है - और हम पहले से नहीं जान सकते कि यह सकारात्मक है या नकारात्मक।

ऐसे में क्या करें? सबसे पहले, हमें इसे एक बार और पूरी तरह से समझ लेना चाहिए यदि समीकरण का दाहिना पक्ष नकारात्मक हो जाता है, तो समीकरण की कोई जड़ नहीं होगी- हम पहले से ही जानते हैं कि मॉड्यूल ऋणात्मक संख्या के बराबर नहीं हो सकता।

और दूसरी बात, यदि दायां हिस्सा अभी भी सकारात्मक है (या शून्य के बराबर है), तो आप पहले की तरह ही कार्य कर सकते हैं: बस मॉड्यूल को प्लस चिह्न के साथ अलग से और माइनस चिह्न के साथ अलग से खोलें।

इस प्रकार, हम मनमाने कार्यों $f\left(x \right)$ और $g\left(x \right)$ के लिए एक नियम बनाते हैं:

\[\बाएं| f\left(x \right) \right|=g\left(x \right)\Rightarrow \left\( \begin(संरेखित)& f\left(x \right)=\pm g\left(x \right) ), \\& g\left(x \right)\ge 0. \\\end(संरेखित) \right.\]

हमारे समीकरण के संबंध में हमें मिलता है:

\[\बाएं| 3x-2 \दाएं|=2x\दायां तीर \बाएं\( \शुरू(संरेखित)& 3x-2=\pm 2x, \\& 2x\ge 0. \\\end(संरेखित) \दाएं.\]

खैर, हम किसी तरह $2x\ge 0$ की आवश्यकता का सामना करेंगे। अंत में, हम मूर्खतापूर्वक उन मूलों को प्रतिस्थापित कर सकते हैं जो हमें पहले समीकरण से प्राप्त होते हैं और जाँच कर सकते हैं कि असमानता कायम है या नहीं।

तो आइए समीकरण को स्वयं हल करें:

\[\begin(संरेखित करें)& 3x-2=2\दायां तीर 3x=4\दायां तीर x=\frac(4)(3); \\& 3x-2=-2\दायां तीर 3x=0\दायां तीर x=0. \\\end(संरेखित करें)\]

खैर, इन दोनों जड़ों में से कौन सी $2x\ge 0$ की आवश्यकता को पूरा करती है? हाँ दोनों! इसलिए, उत्तर दो संख्याएँ होंगी: $x=(4)/(3)\;$ और $x=0$। यही समाधान है :)

मुझे संदेह है कि कुछ छात्र पहले से ही ऊबने लगे हैं? खैर, आइए एक और भी अधिक जटिल समीकरण देखें:

\[\बाएं| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\]

हालाँकि यह बुरा लगता है, वास्तव में यह अभी भी "मापांक बराबर फ़ंक्शन" के रूप का वही समीकरण है:

\[\बाएं| f\left(x \right) \right|=g\left(x \right)\]

और इसे बिल्कुल उसी तरह हल किया जाता है:

\[\बाएं| ((x)^(3))-3((x)^(2))+x \दाएं|=x-((x)^(3))\दायां तीर \बाएं\( \begin(संरेखित करें)& ( (x)^(3))-3((x)^(2))+x=\pm \left(x-((x)^(3)) \right), \\& x-((x )^(3))\ge 0. \\\end(संरेखित) \right.\]

हम असमानता से बाद में निपटेंगे - यह किसी तरह बहुत बुरा है (वास्तव में, यह सरल है, लेकिन हम इसे हल नहीं करेंगे)। अभी के लिए, परिणामी समीकरणों से निपटना बेहतर है। आइए पहले मामले पर विचार करें - यह तब होता है जब मॉड्यूल को प्लस चिह्न के साथ विस्तारित किया जाता है:

\[((x)^(3))-3((x)^(2))+x=x-((x)^(3))\]

खैर, यह कोई दिमाग की बात नहीं है कि आपको बाईं ओर से सब कुछ इकट्ठा करना होगा, समान चीजें लानी होंगी और देखना होगा कि क्या होता है। और यही होता है:

\[\begin(संरेखित करें)& ((x)^(3))-3((x)^(2))+x=x-((x)^(3)); \\& 2((x)^(3))-3((x)^(2))=0; \\\end(संरेखित करें)\]

हम सामान्य गुणनखंड $((x)^(2))$ को कोष्ठक से बाहर निकालते हैं और एक बहुत ही सरल समीकरण प्राप्त करते हैं:

\[((x)^(2))\left(2x-3 \right)=0\दायां तीर \left[ \begin(संरेखित)& ((x)^(2))=0 \\& 2x-3 =0 \\\end(संरेखित करें) \दाएं।\]

\[((x)_(1))=0;\quad ((x)_(2))=\frac(3)(2)=1.5.\]

यहां हमने प्रयोग किया महत्वपूर्ण संपत्तिउत्पाद, जिसके लिए हमने मूल बहुपद का गुणनखंड किया: उत्पाद शून्य के बराबर होता है जब कम से कम एक कारक शून्य के बराबर होता है।

आइए अब दूसरे समीकरण से ठीक उसी तरह निपटें, जो मॉड्यूल को ऋण चिह्न के साथ विस्तारित करके प्राप्त किया जाता है:

\[\begin(संरेखित करें)& ((x)^(3))-3((x)^(2))+x=-\left(x-((x)^(3)) \right); \\& ((x)^(3))-3((x)^(2))+x=-x+((x)^(3)); \\& -3((x)^(2))+2x=0; \\& x\left(-3x+2 \right)=0. \\\end(संरेखित करें)\]

फिर से वही बात: उत्पाद शून्य के बराबर होता है जब कम से कम एक कारक शून्य के बराबर होता है। हमारे पास है:

\[\बाएं[ \शुरू(संरेखित)& x=0 \\& -3x+2=0 \\\अंत(संरेखित) \दाएं।\]

खैर, हमें तीन मूल मिले: $x=0$, $x=1.5$ और $x=(2)/(3)\;$। खैर, इनमें से कौन सा सेट अंतिम उत्तर में जाएगा? ऐसा करने के लिए, याद रखें कि हमारे पास असमानता के रूप में एक अतिरिक्त बाधा है:

इस आवश्यकता को कैसे ध्यान में रखा जाए? आइए बस पाए गए मूलों को प्रतिस्थापित करें और जांचें कि असमानता इन $x$ के लिए है या नहीं। हमारे पास है:

\[\begin(संरेखित करें)& x=0\दायां तीर x-((x)^(3))=0-0=0\ge 0; \\& x=1.5\दायां तीर x-((x)^(3))=1.5-((1.5)^(3)) \lt 0; \\& x=\frac(2)(3)\Rightarrow x-((x)^(3))=\frac(2)(3)-\frac(8)(27)=\frac(10) (27)\ge 0; \\\end(संरेखित करें)\]

इस प्रकार, मूल $x=1.5$ हमारे लिए उपयुक्त नहीं है। और प्रत्युत्तर में केवल दो जड़ें होंगी:

\[((x)_(1))=0;\quad ((x)_(2))=\frac(2)(3).\]

जैसा कि आप देख सकते हैं, इस मामले में भी कुछ भी जटिल नहीं था - मॉड्यूल वाले समीकरण हमेशा एक एल्गोरिदम का उपयोग करके हल किए जाते हैं। आपको बस बहुपदों और असमानताओं की अच्छी समझ होनी चाहिए। इसलिए, हम अधिक जटिल कार्यों की ओर बढ़ते हैं - वहां पहले से ही एक नहीं, बल्कि दो मॉड्यूल होंगे।

दो मॉड्यूल वाले समीकरण

अब तक, हमने केवल सबसे सरल समीकरणों का अध्ययन किया है - एक मॉड्यूल था और कुछ और। हमने इस "कुछ और" को मॉड्यूल से दूर, असमानता के दूसरे हिस्से में भेज दिया, ताकि अंत में सब कुछ $\left| फॉर्म के समीकरण में कम हो जाए। f\left(x \right) \right|=g\left(x \right)$ या इससे भी सरल $\left| f\left(x \right) \right|=a$.

लेकिन KINDERGARTENसमाप्त - अब कुछ अधिक गंभीर बातों पर विचार करने का समय आ गया है। आइए इस तरह के समीकरणों से शुरुआत करें:

\[\बाएं| f\left(x \right) \right|=\left| g\बाएं(x \दाएं) \दाएं|\]

यह "मापांक बराबर मापांक" के रूप का एक समीकरण है। मूलरूप में महत्वपूर्ण बिंदुअन्य नियमों और कारकों की अनुपस्थिति है: बाईं ओर केवल एक मॉड्यूल, दाईं ओर एक और मॉड्यूल - और इससे अधिक कुछ नहीं।

अब कोई यह सोचेगा कि हमने अब तक जो अध्ययन किया है उसकी तुलना में ऐसे समीकरणों को हल करना अधिक कठिन है। लेकिन नहीं: इन समीकरणों को हल करना और भी आसान है। यहाँ सूत्र है:

\[\बाएं| f\left(x \right) \right|=\left| g\left(x \right) \right|\राइटएरो f\left(x \right)=\pm g\left(x \right)\]

सभी! हम बस उनमें से किसी एक के सामने प्लस या माइनस चिह्न लगाकर सबमॉड्यूलर अभिव्यक्तियों को बराबर करते हैं। और फिर हम परिणामी दो समीकरणों को हल करते हैं - और जड़ें तैयार हैं! कोई अतिरिक्त प्रतिबंध, कोई असमानता आदि नहीं। सब कुछ बहुत सरल है.

आइए इस समस्या को हल करने का प्रयास करें:

\[\बाएं| 2x+3 \दाएं|=\बाएं| 2x-7 \दाएं|\]

प्राथमिक वाटसन! मॉड्यूल का विस्तार:

\[\बाएं| 2x+3 \दाएं|=\बाएं| 2x-7 \दाएं|\दायां तीर 2x+3=\pm \बाएं(2x-7 \दाएं)\]

आइए प्रत्येक मामले पर अलग से विचार करें:

\[\begin(संरेखित करें)& 2x+3=2x-7\दायां तीर 3=-7\दायां तीर \emptyset ; \\& 2x+3=-\left(2x-7 \right)\दायां तीर 2x+3=-2x+7. \\\end(संरेखित करें)\]

पहले समीकरण की कोई जड़ नहीं है. क्योंकि $3=-7$ कब है? $x$ के किस मान पर? “$x$ आख़िर क्या है? क्या तुम शराबी हो? वहाँ बिल्कुल भी $x$ नहीं है," आप कहते हैं। और आप सही होंगे. हमने एक समानता प्राप्त की है जो चर $x$ पर निर्भर नहीं करती है, और साथ ही समानता स्वयं गलत है। इसीलिए कोई जड़ें नहीं हैं :)

दूसरे समीकरण के साथ, सब कुछ थोड़ा अधिक दिलचस्प है, लेकिन बहुत, बहुत सरल भी है:

जैसा कि आप देख सकते हैं, सब कुछ शाब्दिक रूप से कुछ पंक्तियों में हल हो गया - हमें रैखिक समीकरण से और कुछ की उम्मीद नहीं थी :)

परिणामस्वरूप, अंतिम उत्तर है: $x=1$।

तो कैसे? कठिन? बिल्कुल नहीं। आइए कुछ और प्रयास करें:

\[\बाएं| x-1 \दाएं|=\बाएं| ((x)^(2))-3x+2 \दाएं|\]

फिर से हमारे पास $\left| के रूप का एक समीकरण है f\left(x \right) \right|=\left| g\left(x \right) \right|$. इसलिए, हम मापांक चिह्न को प्रकट करते हुए तुरंत इसे फिर से लिखते हैं:

\[((x)^(2))-3x+2=\pm \left(x-1 \right)\]

शायद अब कोई पूछेगा: “अरे, क्या बकवास है? "प्लस-माइनस" दाएँ हाथ की अभिव्यक्ति पर क्यों दिखाई देता है और बाईं ओर नहीं?" शांत हो जाओ, मैं अब सब कुछ समझाऊंगा। वास्तव में, अच्छे तरीके से हमें अपने समीकरण को इस प्रकार फिर से लिखना चाहिए था:

फिर आपको कोष्ठक खोलने होंगे, सभी पदों को समान चिह्न के एक तरफ ले जाना होगा (चूंकि समीकरण, जाहिर है, दोनों मामलों में वर्ग होगा), और फिर मूल खोजें। लेकिन आपको स्वीकार करना होगा: जब "प्लस-माइनस" तीन शब्दों से पहले आता है (विशेषकर जब इनमें से एक शब्द द्विघात अभिव्यक्ति है), तो यह किसी भी तरह उस स्थिति से अधिक जटिल लगता है जब "प्लस-माइनस" केवल दो शब्दों से पहले आता है।

लेकिन कोई भी चीज़ हमें मूल समीकरण को इस प्रकार दोबारा लिखने से नहीं रोकती:

\[\बाएं| x-1 \दाएं|=\बाएं| ((x)^(2))-3x+2 \दाएं|\दायां तीर \बाएं| ((x)^(2))-3x+2 \दाएं|=\बाएं| x-1 \दाएं|\]

क्या हुआ? कुछ खास नहीं: उन्होंने बस बाएँ और दाएँ पक्षों की अदला-बदली की। एक छोटी सी चीज़ जो अंततः हमारे जीवन को थोड़ा आसान बना देगी :)

सामान्य तौर पर, हम प्लस और माइनस वाले विकल्पों पर विचार करके इस समीकरण को हल करते हैं:

\[\begin(संरेखित करें)& ((x)^(2))-3x+2=x-1\दायां तीर ((x)^(2))-4x+3=0; \\& ((x)^(2))-3x+2=-\left(x-1 \right)\Rightarrow ((x)^(2))-2x+1=0. \\\end(संरेखित करें)\]

पहले समीकरण के मूल $x=3$ और $x=1$ हैं। दूसरा आम तौर पर एक सटीक वर्ग होता है:

\[((x)^(2))-2x+1=((\left(x-1 \right))^(2))\]

इसलिए, इसका केवल एक ही मूल है: $x=1$। परंतु यह मूल हमें पहले ही प्राप्त हो चुका है। इस प्रकार, अंतिम उत्तर में केवल दो संख्याएँ शामिल होंगी:

\[((x)_(1))=3;\quad ((x)_(2))=1.\]

मिशन पूरा! आप शेल्फ से एक पाई ले सकते हैं और खा सकते हैं। उनमें से 2 हैं, आपका बीच वाला है :)

महत्वपूर्ण लेख. के लिए समान जड़ों की उपस्थिति विभिन्न विकल्पमापांक के विस्तार का मतलब है कि मूल बहुपद गुणनखंडित हैं, और इन कारकों के बीच निश्चित रूप से एक सामान्य कारक होगा। वास्तव में:

\[\शुरू(संरेखित करें)& \बाएं| x-1 \दाएं|=\बाएं| ((x)^(2))-3x+2 \दाएं|; \\& \बाएं| x-1 \दाएं|=\बाएं| \बाएं(x-1 \दाएं)\बाएं(x-2 \दाएं) \दाएं| \\\end(संरेखित करें)\]

मॉड्यूल गुणों में से एक: $\left| a\cdot b \दाएं|=\बाएं| एक \दाएं|\cdot \बाएं| b \right|$ (अर्थात् उत्पाद का मापांक मापांक के गुणनफल के बराबर है), इसलिए मूल समीकरण को निम्नानुसार फिर से लिखा जा सकता है:

\[\बाएं| x-1 \दाएं|=\बाएं| x-1 \दाएं|\cdot \बाएं| x-2 \दाएं|\]

जैसा कि आप देख सकते हैं, हमारे पास वास्तव में एक सामान्य कारक है। अब, यदि आप सभी मॉड्यूल को एक तरफ इकट्ठा करते हैं, तो आप इस कारक को ब्रैकेट से बाहर निकाल सकते हैं:

\[\शुरू(संरेखित करें)& \बाएं| x-1 \दाएं|=\बाएं| x-1 \दाएं|\cdot \बाएं| x-2 \दाएँ|; \\& \बाएं| x-1 \दाएं|-\बाएं| x-1 \दाएं|\cdot \बाएं| x-2 \दाएं|=0; \\& \बाएं| x-1 \दाएं|\cdot \बाएं(1-\बाएं| x-2 \दाएं| \दाएं)=0. \\\end(संरेखित करें)\]

खैर, अब याद रखें कि उत्पाद शून्य के बराबर है जब कम से कम एक कारक शून्य के बराबर है:

\[\बाएं[ \शुरू(संरेखित करें)& \बाएं| x-1 \दाएं|=0, \\& \बाएं| x-2 \दाएं|=1. \\\end(संरेखित करें) \दाएं।\]

इस प्रकार, दो मॉड्यूल वाले मूल समीकरण को दो सरलतम समीकरणों में बदल दिया गया है जिनके बारे में हमने पाठ की शुरुआत में बात की थी। ऐसे समीकरणों को वस्तुतः कुछ पंक्तियों में हल किया जा सकता है :)

यह टिप्पणी व्यवहार में अनावश्यक रूप से जटिल और अनुपयुक्त लग सकती है। हालाँकि, वास्तव में, आप उन समस्याओं से कहीं अधिक जटिल समस्याओं का सामना कर सकते हैं जिन्हें हम आज देख रहे हैं। उनमें, मॉड्यूल को बहुपदों के साथ जोड़ा जा सकता है, अंकगणितीय जड़ें, लघुगणक, आदि। और ऐसी स्थितियों में, कोष्ठक से कुछ निकालकर समीकरण की समग्र डिग्री को कम करने की क्षमता बहुत उपयोगी हो सकती है :)

अब मैं एक और समीकरण का विश्लेषण करना चाहूंगा, जो पहली नज़र में अजीब लग सकता है। कई छात्र इस पर अटक जाते हैं, यहां तक ​​कि वे भी जो सोचते हैं कि उन्हें मॉड्यूल की अच्छी समझ है।

हालाँकि, इस समीकरण को हल करना उससे भी आसान है जिसे हमने पहले देखा था। और यदि आप इसका कारण समझते हैं, तो आपको मॉड्यूली के साथ समीकरणों को शीघ्रता से हल करने के लिए एक और तरकीब मिल जाएगी।

तो समीकरण यह है:

\[\बाएं| x-((x)^(3)) \दाएं|+\बाएं| ((x)^(2))+x-2 \दाएं|=0\]

नहीं, यह कोई टाइपो त्रुटि नहीं है: यह मॉड्यूल के बीच एक प्लस है। और हमें यह पता लगाना होगा कि $x$ पर दो मॉड्यूल का योग शून्य के बराबर है :)

आखिर समस्या क्या है? लेकिन समस्या यह है कि प्रत्येक मॉड्यूल एक सकारात्मक संख्या है, या चरम मामलों में, शून्य है। यदि आप दो धनात्मक संख्याएँ जोड़ दें तो क्या होगा? जाहिर है फिर से एक सकारात्मक संख्या:

\[\begin(संरेखित करें)& 5+7=12 \gt 0; \\& 0.004+0.0001=0.0041 \gt 0; \\& 5+0=5 \gt 0. \\\end(संरेखित)\]

अंतिम पंक्ति आपको एक विचार दे सकती है: मॉड्यूल का योग केवल तभी शून्य होता है जब प्रत्येक मॉड्यूल शून्य होता है:

\[\बाएं| x-((x)^(3)) \दाएं|+\बाएं| ((x)^(2))+x-2 \दाएं|=0\दायां तीर \बाएं\( \begin(संरेखित)& \बाएं| x-((x)^(3)) \दाएं|=0, \\& \बाएं|. ((x)^(2))+x-2 \दाएं|=0. \\\end(संरेखित) \दाएं.\]

और मॉड्यूल शून्य के बराबर कब है? केवल एक मामले में - जब सबमॉड्यूलर अभिव्यक्ति शून्य के बराबर है:

\[((x)^(2))+x-2=0\दायां तीर \बाएं(x+2 \दाएं)\बाएं(x-1 \दाएं)=0\दायां तीर \बाएं[ \शुरू(संरेखित)& x=-2 \\& x=1 \\\end(संरेखित) \दाएं.\]

इस प्रकार, हमारे पास तीन बिंदु हैं जिन पर पहला मॉड्यूल शून्य पर रीसेट हो गया है: 0, 1 और -1; साथ ही दो बिंदु जहां दूसरे मॉड्यूल को शून्य पर रीसेट किया जाता है: -2 और 1. हालांकि, हमें एक ही समय में दोनों मॉड्यूल को शून्य पर रीसेट करने की आवश्यकता है, इसलिए पाए गए नंबरों में से हमें उन लोगों को चुनने की ज़रूरत है जो इसमें शामिल हैं दोनों सेट. जाहिर है, ऐसी केवल एक ही संख्या है: $x=1$ - यह अंतिम उत्तर होगा।

विच्छेदन विधि

ख़ैर, हमने पहले ही ढेर सारी समस्याओं को कवर कर लिया है और बहुत सारी तकनीकें सीख ली हैं। क्या आपको लगता है कि बस इतना ही है? लेकिन कोई नहीं! अब हम अंतिम तकनीक को देखेंगे - और साथ ही सबसे महत्वपूर्ण भी। हम मापांक के साथ समीकरणों को विभाजित करने के बारे में बात करेंगे। हम बात भी क्या करेंगे? आइए थोड़ा पीछे जाएं और कुछ सरल समीकरण देखें। उदाहरण के लिए यह:

\[\बाएं| 3x-5 \दाएं|=5-3x\]

सिद्धांत रूप में, हम पहले से ही जानते हैं कि ऐसे समीकरण को कैसे हल किया जाए, क्योंकि यह $\left| फॉर्म का एक मानक निर्माण है f\left(x \right) \right|=g\left(x \right)$. लेकिन आइए इस समीकरण को थोड़ा अलग कोण से देखने का प्रयास करें। अधिक सटीक रूप से, मापांक चिह्न के अंतर्गत अभिव्यक्ति पर विचार करें। मैं आपको याद दिला दूं कि किसी भी संख्या का मापांक स्वयं उस संख्या के बराबर हो सकता है, या यह इस संख्या के विपरीत भी हो सकता है:

\[\बाएं| a \right|=\left\( \begin(संरेखित)& a,\quad a\ge 0, \\& -a,\quad a \lt 0. \\\end(संरेखित) \right.\]

दरअसल, यह अस्पष्टता ही पूरी समस्या है: चूंकि मापांक के तहत संख्या बदलती है (यह चर पर निर्भर करती है), यह हमारे लिए स्पष्ट नहीं है कि यह सकारात्मक है या नकारात्मक।

लेकिन क्या होगा यदि आपको प्रारंभ में यह आवश्यकता हो कि यह संख्या सकारात्मक हो? उदाहरण के लिए, आइए $3x-5 \gt 0$ की आवश्यकता है - इस मामले में हमें मापांक चिह्न के तहत एक सकारात्मक संख्या प्राप्त करने की गारंटी है, और हम इस मापांक से पूरी तरह से छुटकारा पा सकते हैं:

इस प्रकार, हमारा समीकरण एक रैखिक समीकरण में बदल जाएगा, जिसे आसानी से हल किया जा सकता है:

सच है, ये सभी विचार केवल $3x-5 \gt 0$ की स्थिति के तहत ही समझ में आते हैं - मॉड्यूल को स्पष्ट रूप से प्रकट करने के लिए हमने स्वयं इस आवश्यकता को पेश किया है। इसलिए, आइए पाए गए $x=\frac(5)(3)$ को इस स्थिति में प्रतिस्थापित करें और जांचें:

यह पता चला है कि $x$ के निर्दिष्ट मूल्य के लिए हमारी आवश्यकता पूरी नहीं हुई है, क्योंकि अभिव्यक्ति शून्य के बराबर निकली, और हमें इसकी आवश्यकता शून्य से अधिक होनी चाहिए। उदास। :(

लेकिन कोई बात नहीं! आख़िरकार, एक और विकल्प भी है $3x-5 \lt 0$। इसके अलावा: $3x-5=0$ का मामला भी है - इस पर भी विचार करने की आवश्यकता है, अन्यथा समाधान अधूरा होगा। तो, मामले पर विचार करें $3x-5 \lt 0$:

जाहिर है, मॉड्यूल ऋण चिह्न के साथ खुलेगा। लेकिन तब एक अजीब स्थिति उत्पन्न होती है: मूल समीकरण में बाएँ और दाएँ दोनों तरफ एक ही अभिव्यक्ति दिखाई देगी:

मुझे आश्चर्य है कि किस $x$ पर अभिव्यक्ति $5-3x$ अभिव्यक्ति $5-3x$ के बराबर होगी? ऐसे समीकरणों से कैप्टन ओब्विअसनेस का गला भी घुट जाएगा, लेकिन हम जानते हैं: यह समीकरण एक पहचान है, यानी। यह चर के किसी भी मान के लिए सत्य है!

इसका मतलब यह है कि कोई भी $x$ हमारे लिए उपयुक्त होगा। हालाँकि, हमारी एक सीमा है:

दूसरे शब्दों में, उत्तर एक संख्या नहीं, बल्कि एक संपूर्ण अंतराल होगा:

अंततः, विचार करने के लिए एक और मामला बचा है: $3x-5=0$। यहां सब कुछ सरल है: मापांक के अंतर्गत शून्य होगा, और शून्य का मापांक भी शून्य के बराबर है (यह सीधे परिभाषा से अनुसरण करता है):

लेकिन फिर मूल समीकरण $\बाएं| 3x-5 \right|=5-3x$ को इस प्रकार पुनः लिखा जाएगा:

जब हमने $3x-5 \gt 0$ के मामले पर विचार किया तो हम पहले ही यह मूल प्राप्त कर चुके हैं। इसके अलावा, यह रूट समीकरण $3x-5=0$ का एक समाधान है - यह वह सीमा है जिसे हमने मॉड्यूल को रीसेट करने के लिए स्वयं पेश किया है :)

इस प्रकार, अंतराल के अतिरिक्त, हम इस अंतराल के बिल्कुल अंत में स्थित संख्या से भी संतुष्ट होंगे:

मॉड्यूलो समीकरणों में जड़ों का संयोजन

कुल अंतिम उत्तर: $x\in \left(-\infty ;\frac(5)(3) \right]$ मापांक के साथ काफी सरल (अनिवार्य रूप से रैखिक) समीकरण के उत्तर में ऐसी बकवास देखना बहुत आम नहीं है, वास्तव में? खैर, इसकी आदत डालें: मॉड्यूल की कठिनाई यह है कि ऐसे समीकरणों में उत्तर पूरी तरह से अप्रत्याशित हो सकते हैं।

कुछ और अधिक महत्वपूर्ण है: हमने एक मापांक के साथ समीकरण को हल करने के लिए एक सार्वभौमिक एल्गोरिदम का विश्लेषण किया है! और इस एल्गोरिदम में निम्नलिखित चरण शामिल हैं:

1. समीकरण में प्रत्येक मापांक को शून्य के बराबर करें। हमें कई समीकरण मिलते हैं;
2. इन सभी समीकरणों को हल करें और संख्या रेखा पर मूल अंकित करें। परिणामस्वरूप, सीधी रेखा को कई अंतरालों में विभाजित किया जाएगा, जिनमें से प्रत्येक पर सभी मॉड्यूल विशिष्ट रूप से प्रकट होंगे;
3. प्रत्येक अंतराल के लिए मूल समीकरण को हल करें और अपने उत्तरों को संयोजित करें।

बस इतना ही! केवल एक ही प्रश्न बचा है: चरण 1 में प्राप्त जड़ों का क्या करें? मान लीजिए कि हमारी दो जड़ें हैं: $x=1$ और $x=5$। वे संख्या रेखा को 3 टुकड़ों में विभाजित करेंगे:

बिंदुओं का उपयोग करके संख्या रेखा को अंतरालों में विभाजित करना

तो अंतराल क्या हैं? यह स्पष्ट है कि उनमें से तीन हैं:

1. सबसे बाईं ओर वाला: $x \lt 1$ - इकाई स्वयं अंतराल में शामिल नहीं है;
2. सेंट्रल: $1\le x \lt 5$ - यहां एक को अंतराल में शामिल किया गया है, लेकिन पांच को शामिल नहीं किया गया है;
3. सबसे दाहिना: $x\ge 5$ - पाँच केवल यहाँ शामिल है!

मुझे लगता है कि आप पैटर्न को पहले से ही समझ गए हैं। प्रत्येक अंतराल में बायां छोर शामिल है और दायां शामिल नहीं है।

पहली नज़र में, ऐसी प्रविष्टि असुविधाजनक, अतार्किक और आम तौर पर किसी प्रकार की पागलपन भरी लग सकती है। लेकिन मेरा विश्वास करें: थोड़े अभ्यास के बाद, आप पाएंगे कि यह दृष्टिकोण सबसे विश्वसनीय है और मॉड्यूल को स्पष्ट रूप से खोलने में हस्तक्षेप नहीं करता है। हर बार सोचने की तुलना में ऐसी योजना का उपयोग करना बेहतर है: वर्तमान अंतराल को बाएँ/दाएँ छोर दें या इसे अगले में "फेंक" दें।

यह ऑनलाइन गणित कैलकुलेटर आपकी मदद करेगा मॉड्यूली के साथ समीकरण या असमानता को हल करें. के लिए कार्यक्रम मापांक के साथ समीकरणों और असमानताओं को हल करनान केवल समस्या का उत्तर देता है, बल्कि नेतृत्व भी करता है स्पष्टीकरण के साथ विस्तृत समाधान, अर्थात। परिणाम प्राप्त करने की प्रक्रिया प्रदर्शित करता है।

यह कार्यक्रम हाई स्कूल के विद्यार्थियों के लिए उपयोगी हो सकता है माध्यमिक स्कूलोंतैयारी के लिए परीक्षणऔर परीक्षा, जब माता-पिता के लिए गणित और बीजगणित में कई समस्याओं के समाधान को नियंत्रित करने के लिए एकीकृत राज्य परीक्षा से पहले ज्ञान का परीक्षण किया जाता है। या हो सकता है कि आपके लिए ट्यूटर नियुक्त करना या नई पाठ्यपुस्तकें खरीदना बहुत महंगा हो? या क्या आप इसे यथाशीघ्र पूरा करना चाहते हैं? गृहकार्यगणित में या बीजगणित में? इस मामले में, आप विस्तृत समाधानों के साथ हमारे कार्यक्रमों का भी उपयोग कर सकते हैं।

इस तरह आप अपना स्वयं का प्रशिक्षण और/या अपना प्रशिक्षण संचालित कर सकते हैं। छोटे भाईया बहनें, जबकि समस्याओं के समाधान के क्षेत्र में शिक्षा का स्तर बढ़ता है।

|x| या एबीएस (एक्स) - मॉड्यूल एक्स

मॉड्यूलि के साथ एक समीकरण या असमानता दर्ज करें

किसी समीकरण या असमानता को हल करें

यह पाया गया कि इस समस्या को हल करने के लिए आवश्यक कुछ स्क्रिप्ट लोड नहीं की गईं, और प्रोग्राम काम नहीं कर सकता है।
हो सकता है कि आपके पास AdBlock सक्षम हो.
इस स्थिति में, इसे अक्षम करें और पृष्ठ को ताज़ा करें।

आपके ब्राउजर में जावास्क्रिप्ट अक्षम है।
समाधान प्रकट करने के लिए, आपको जावास्क्रिप्ट सक्षम करना होगा।
यहां आपके ब्राउज़र में जावास्क्रिप्ट को सक्षम करने के निर्देश दिए गए हैं।

क्योंकि समस्या का समाधान करने के इच्छुक बहुत से लोग हैं, आपका अनुरोध कतारबद्ध हो गया है।
कुछ ही सेकंड में समाधान नीचे दिखाई देगा.
कृपया प्रतीक्षा करें सेकंड...

अगर आप समाधान में एक त्रुटि देखी गई, तो आप इसके बारे में फीडबैक फॉर्म में लिख सकते हैं।
भूलना नहीं बताएं कि कौन सा कार्य हैआप तय करें क्या फ़ील्ड में प्रवेश करें.

हमारे गेम, पहेलियाँ, एमुलेटर:

थोड़ा सिद्धांत.

मापांक के साथ समीकरण और असमानताएँ

बुनियादी स्कूल बीजगणित पाठ्यक्रम में, आप मॉड्यूली के साथ सबसे सरल समीकरणों और असमानताओं का सामना कर सकते हैं। उन्हें हल करने के लिए, आप इस तथ्य के आधार पर एक ज्यामितीय विधि का उपयोग कर सकते हैं कि \(|x-a| \) बिंदु x और a के बीच संख्या रेखा पर दूरी है: \(|x-a| = \rho (x;\; a) \). उदाहरण के लिए, समीकरण \(|x-3|=2\) को हल करने के लिए आपको संख्या रेखा पर ऐसे बिंदु ढूंढने होंगे जो बिंदु 3 से 2 की दूरी पर हों। ऐसे दो बिंदु हैं: \(x_1=1 \) और \(x_2=5\) .

असमानता को हल करना \(|2x+7|

लेकिन मापांक के साथ समीकरणों और असमानताओं को हल करने का मुख्य तरीका तथाकथित "परिभाषा के अनुसार मापांक का रहस्योद्घाटन" से जुड़ा है:
यदि \(a \geq 0 \), तो \(|a|=a \);
यदि \(a एक नियम के रूप में, मापांक के साथ एक समीकरण (असमानता) को समीकरणों (असमानताओं) के एक सेट में घटा दिया जाता है जिसमें मापांक चिह्न नहीं होता है।

उपरोक्त परिभाषा के अतिरिक्त, निम्नलिखित कथनों का उपयोग किया जाता है:
1) यदि \(c > 0\), तो समीकरण \(|f(x)|=c \) समीकरणों के सेट के बराबर है: \(\left[\begin(array)(l) f(x) )=c \\ f(x)=-c \end(array)\right.
2) यदि \(c > 0 \), तो असमानता \(|f(x)| 3) यदि \(c \geq 0 \), तो असमानता \(|f(x)| > c \) है असमानताओं के एक सेट के बराबर: \(\left[\begin(array)(l) f(x) c \end(array)\right. \)
4) यदि असमानता के दोनों पक्ष \(f(x) उदाहरण 1. समीकरण \(x^2 +2|x-1| -6 = 0\) को हल करें।

यदि \(x-1 \geq 0\), तो \(|x-1| = x-1\) और दिया गया समीकरण रूप लेता है
\(x^2 +2(x-1) -6 = 0 \राइटएरो x^2 +2x -8 = 0 \).
यदि \(x-1 \(x^2 -2(x-1) -6 = 0 \राइटएरो x^2 -2x -4 = 0 \).
इस प्रकार, दिए गए समीकरण पर प्रत्येक दो संकेतित मामलों में अलग से विचार किया जाना चाहिए।
1) मान लीजिए \(x-1 \geq 0 \), अर्थात्। \(x\geq 1\). समीकरण \(x^2 +2x -8 = 0\) से हम \(x_1=2, \; x_2=-4\) पाते हैं। शर्त \(x \geq 1 \) केवल \(x_1=2\) मान से संतुष्ट होती है।
2) मान लीजिए \(x-1 उत्तर: \(2; \;\; 1-\sqrt(5) \)

उदाहरण 2. समीकरण \(|x^2-6x+7| = \frac(5x-9)(3)\) को हल करें।

पहला तरीका(परिभाषा के अनुसार मॉड्यूल विस्तार)।
उदाहरण 1 के अनुसार तर्क करते हुए, हम इस निष्कर्ष पर पहुंचते हैं कि यदि दो शर्तें पूरी होती हैं तो दिए गए समीकरण पर अलग से विचार करने की आवश्यकता है: \(x^2-6x+7 \geq 0 \) या \(x^2-6x+7

1) यदि \(x^2-6x+7 \geq 0 \), तो \(|x^2-6x+7| = x^2-6x+7 \) और दिया गया समीकरण \(x) का रूप लेता है ^2 -6x+7 = \frac(5x-9)(3) \दायां तीर 3x^2-23x+30=0 \). ये तय कर लिया द्विघात समीकरण, हमें मिलता है: \(x_1=6, \; x_2=\frac(5)(3) \).
आइए जानें कि क्या मान \(x_1=6\) शर्त \(x^2-6x+7 \geq 0\) को संतुष्ट करता है। ऐसा करने के लिए, संकेतित मान को द्विघात असमानता में प्रतिस्थापित करें। हमें मिलता है: \(6^2-6 \cdot 6+7 \geq 0 \), यानी। \(7 \geq 0 \) एक सच्ची असमानता है। इसका मतलब है कि \(x_1=6\) दिए गए समीकरण का मूल है।
आइए जानें कि क्या मान \(x_2=\frac(5)(3)\) शर्त \(x^2-6x+7 \geq 0\) को संतुष्ट करता है। ऐसा करने के लिए, संकेतित मान को द्विघात असमानता में प्रतिस्थापित करें। हमें मिलता है: \(\left(\frac(5)(3) \right)^2 -\frac(5)(3) \cdot 6 + 7 \geq 0 \), यानी। \(\frac(25)(9) -3 \geq 0 \) एक गलत असमानता है। इसका मतलब यह है कि \(x_2=\frac(5)(3)\) दिए गए समीकरण का मूल नहीं है।

2) यदि \(x^2-6x+7 मान \(x_3=3\) शर्त को संतुष्ट करता है \(x^2-6x+7 मान \(x_4=\frac(4)(3) \) संतुष्ट नहीं करता है स्थिति \ (x^2-6x+7 तो, दिए गए समीकरण के दो मूल हैं: \(x=6, \; x=3 \).

दूसरा तरीका.यदि समीकरण \(|f(x)| = h(x) \) दिया गया है, तो \(h(x) \(\left[\begin(array)(l) x^2-6x+7 = के साथ \frac (5x-9)(3) \\ x^2-6x+7 = -\frac(5x-9)(3) \end(array)\right \)
इन दोनों समीकरणों को ऊपर हल किया गया था (दिए गए समीकरण को हल करने की पहली विधि का उपयोग करके), उनकी जड़ें इस प्रकार हैं: \(6,\; \frac(5)(3),\; 3,\; \frac(4) )(3)\). इनसे स्थिति \(\frac(5x-9)(3) \geq 0 \). चार मूल्यकेवल दो को संतुष्ट करें: 6 और 3. इसका मतलब है कि दिए गए समीकरण के दो मूल हैं: \(x=6, \; x=3\).

तीसरा तरीका(ग्राफिक)।
1) आइए फ़ंक्शन \(y = |x^2-6x+7| \) का एक ग्राफ़ बनाएं। सबसे पहले, आइए एक परवलय \(y = x^2-6x+7\) बनाएं। हमारे पास \(x^2-6x+7 = (x-3)^2-2 \) है। फ़ंक्शन \(y = (x-3)^2-2\) का ग्राफ़ फ़ंक्शन \(y = x^2\) के ग्राफ़ से 3 स्केल इकाइयों को दाईं ओर स्थानांतरित करके प्राप्त किया जा सकता है (साथ में) x-अक्ष) और 2 स्केल इकाइयाँ नीचे (y-अक्ष के अनुदिश)। सीधी रेखा x=3 उस परवलय की धुरी है जिसमें हम रुचि रखते हैं। जैसा नियंत्रण केंद्रअधिक सटीक आलेखन के लिए, बिंदु (3; -2) - परवलय का शीर्ष, बिंदु (0; 7) और बिंदु (6; 7) को परवलय के अक्ष के सापेक्ष सममित लेना सुविधाजनक है।
अब फ़ंक्शन \(y = |x^2-6x+7| \) का ग्राफ़ बनाने के लिए, आपको निर्मित परवलय के उन हिस्सों को अपरिवर्तित छोड़ना होगा जो x-अक्ष के नीचे नहीं हैं, और उस हिस्से को प्रतिबिंबित करना होगा परवलय जो x-अक्ष के सापेक्ष x-अक्ष के नीचे स्थित होता है।
2) चलिए एक ग्राफ बनाते हैं रैखिक प्रकार्य\(y = \frac(5x-9)(3)\). अंक (0; -3) और (3; 2) को नियंत्रण बिंदु के रूप में लेना सुविधाजनक है।

यह महत्वपूर्ण है कि भुज अक्ष के साथ सीधी रेखा के प्रतिच्छेदन का बिंदु x = 1.8, भुज अक्ष के साथ परवलय के प्रतिच्छेदन के बाएं बिंदु के दाईं ओर स्थित है - यह बिंदु \(x=3-\) है sqrt(2) \) (चूंकि \(3-\sqrt(2 ) 3) रेखाचित्र को देखते हुए, ग्राफ़ दो बिंदुओं - A(3; 2) और B(6; 7) पर प्रतिच्छेद करते हैं। इनके भुजाओं को प्रतिस्थापित करते हुए दिए गए समीकरण में अंक x = 3 और x = 6, हम आश्वस्त हैं कि दोनों मामलों में, सही संख्यात्मक समानता प्राप्त होती है। इसका मतलब है कि हमारी परिकल्पना की पुष्टि की गई है - समीकरण की दो जड़ें हैं: x = 3 और x = 6. उत्तर: 3;

टिप्पणी. ग्राफ़िक विधिअपनी सारी सुंदरता के बावजूद, यह बहुत विश्वसनीय नहीं है। विचारित उदाहरण में, यह केवल इसलिए काम करता है क्योंकि समीकरण की जड़ें पूर्णांक हैं।

उदाहरण 3. समीकरण को हल करें \(|2x-4|+|x+3| = 8\)

पहला तरीका
अभिव्यक्ति 2x-4 बिंदु x = 2 पर 0 हो जाती है, और अभिव्यक्ति x + 3 बिंदु x = -3 पर 0 हो जाती है। ये दो बिंदु संख्या रेखा को तीन अंतरालों में विभाजित करते हैं: \(x

पहले अंतराल पर विचार करें: \((-\infty; \; -3) \).
यदि x दूसरे अंतराल पर विचार करें: \([-3; \; 2) \).
यदि \(-3 \leq x तीसरे अंतराल पर विचार करें: \(। अब हम x>2.5 के लिए आंतरिक मॉड्यूल का विस्तार करते हैं। हम एक मॉड्यूल के साथ एक समीकरण प्राप्त करते हैं
|2x-5-1|=x+3;
|2x-6|=x+3.
मॉड्यूल का विस्तार करते समय हमें निम्नलिखित मिलता है रेखीय समीकरण
-2x+6=x+3 या 2x-6=x+3;
2x+x=6-3 या 2x-x=3+6;
3x=3; x=1 या x=9 .
पहला मान x=1 शर्त x>2.5 को संतुष्ट नहीं करता है। तो इस अंतराल पर हमारे पास मापांक x=9 वाले समीकरण का एक मूल है, और कुल मिलाकर दो हैं (x=1/3)। प्रतिस्थापन द्वारा आप की गई गणना की शुद्धता की जांच कर सकते हैं
उत्तर: x=1/3; एक्स=9.

उदाहरण 4. दोहरे मॉड्यूल का समाधान खोजें ||3x-1|-5|=2x-3.
समाधान: आइए समीकरण के आंतरिक मॉड्यूल का विस्तार करें
|3x-1|=0 <=>एक्स=1/3.
बिंदु x=2.5 संख्या रेखा को दो अंतरालों में और दिए गए समीकरण को दो मामलों में विभाजित करता है। हम समीकरण के स्वरूप के आधार पर समाधान की शर्त लिखते हैं दाहिनी ओर
2x-3>=0 ->x>=3/2=1.5.
इससे यह पता चलता है कि हम >=1.5 मूल्यों में रुचि रखते हैं। इस प्रकार मॉड्यूलर समीकरणदो अंतरालों पर विचार करें
,
|-(3x-1)-5|=2x-3;
|-3x-4|=2x-3.
परिणामी मॉड्यूल, विस्तारित होने पर, 2 समीकरणों में विभाजित हो जाता है
-3x-4=2x-3 या 3x+4=2x-3;
2x+3x=-4+3 या 3x-2x=-3-4;
5x=-1; x=-1/5 या x=-7 .
दोनों मान अंतराल में नहीं आते हैं, यानी वे मॉड्यूलि वाले समीकरण के समाधान नहीं हैं। इसके बाद, हम x>2.5 के लिए मॉड्यूल का विस्तार करेंगे। हमें निम्नलिखित समीकरण प्राप्त होता है
|3x-1-5|=2x-3;
|3x-6|=2x-3.
मॉड्यूल का विस्तार करने पर, हमें 2 रैखिक समीकरण मिलते हैं
3x-6=2x-3 या –(3x-6)=2x-3;
3x-2x=-3+6या 2x+3x=6+3;
x=3 या 5x=9; x=9/5=1.8.
पाया गया दूसरा मान x>2.5 शर्त के अनुरूप नहीं है, हम इसे अस्वीकार करते हैं।
अंततः हमारे पास मॉड्यूल x=3 वाले समीकरण का एक मूल है।
जाँच करना
||3*3-1|-5|=2*3-3 3=3 .
मापांक के साथ समीकरण के मूल की गणना सही ढंग से की गई थी।
उत्तर: x=1/3; एक्स=9.

एमबीओयू सेकेंडरी स्कूल नंबर 17, इवानोवो

« मापांक के साथ समीकरण"
पद्धतिगत विकास

संकलित

गणित शिक्षक

लेबेदेवा एन.वी.

20010

व्याख्यात्मक नोट

अध्याय 1 परिचय

धारा 2. मूल गुण धारा 3. किसी संख्या के मापांक की अवधारणा की ज्यामितीय व्याख्या धारा 4. फ़ंक्शन का ग्राफ़ y = |x| धारा 5. कन्वेंशन

अध्याय 2. मापांक वाले समीकरणों को हल करना

धारा 1. फॉर्म के समीकरण |F(x)| = एम (सरलतम) धारा 2. F(|x|) = m के रूप के समीकरण धारा 3. फॉर्म के समीकरण |F(x)| = जी(एक्स) धारा 4. फॉर्म के समीकरण |F(x)| = ± एफ(एक्स) (सबसे सुंदर) धारा 5. फॉर्म के समीकरण |F(x)| = |जी(एक्स)| धारा 6. गैर-मानक समीकरणों को हल करने के उदाहरण धारा 7. फॉर्म के समीकरण |F(x)| + |जी(एक्स)| = 0 धारा 8. फॉर्म के समीकरण |a 1 x ± b 1 | ± |ए 2 एक्स ± बी 2 | ± …|a n x ± in n | = एम धारा 9. कई मॉड्यूल वाले समीकरण

अध्याय 3. मापांक के साथ विभिन्न समीकरणों को हल करने के उदाहरण।

धारा 1. त्रिकोणमितीय समीकरण धारा 2. घातीय समीकरण धारा 3। लघुगणकीय समीकरण धारा 4. अपरिमेय समीकरण धारा 5. असाइनमेंट बढ़ी हुई जटिलता अभ्यासों के उत्तर ग्रन्थसूची

व्याख्यात्मक नोट.

किसी वास्तविक संख्या के निरपेक्ष मान (मापांक) की अवधारणा इसकी आवश्यक विशेषताओं में से एक है। यह अवधारणा भौतिक, गणितीय और तकनीकी विज्ञान के विभिन्न वर्गों में व्यापक है। गणित पाठ्यक्रम पढ़ाने के अभ्यास में हाई स्कूलरूसी संघ के रक्षा मंत्रालय के कार्यक्रम के अनुसार, "किसी संख्या का पूर्ण मूल्य" की अवधारणा बार-बार प्रकट होती है: 6 वीं कक्षा में, एक मॉड्यूल की परिभाषा पेश की जाती है, इसकी ज्यामितीय अर्थ; आठवीं कक्षा में पूर्ण त्रुटि की अवधारणा बनती है, सरलतम समीकरणों और मापांक युक्त असमानताओं के समाधान पर विचार किया जाता है, अंकगणित के गुणों का अध्ययन किया जाता है वर्गमूल; 11वीं कक्षा में यह अवधारणा "रूट" खंड में पाई जाती है एन-वीं डिग्री।"शिक्षण अनुभव से पता चलता है कि ज्ञान की आवश्यकता वाले कार्यों को हल करते समय छात्रों को अक्सर कठिनाइयों का सामना करना पड़ता है इस सामग्री का, और अक्सर वे इसे लागू करना शुरू किए बिना ही इसे छोड़ देते हैं। ग्रंथों में परीक्षा कार्यइसी तरह के कार्य 9वीं और 11वीं कक्षा के पाठ्यक्रमों के लिए भी शामिल हैं। इसके अलावा, विश्वविद्यालय स्कूली स्नातकों पर जो अपेक्षाएं रखते हैं, वे अलग-अलग होती हैं, अर्थात् अधिक उच्च स्तरस्कूली पाठ्यक्रम की आवश्यकताओं की तुलना में। जीवन के लिए आधुनिक समाजगणितीय सोच शैली विकसित करना बहुत महत्वपूर्ण है, जो कुछ मानसिक कौशलों में प्रकट होती है। मॉड्यूल के साथ समस्याओं को हल करने की प्रक्रिया में, सामान्यीकरण और विनिर्देश, विश्लेषण, वर्गीकरण और व्यवस्थितकरण, और सादृश्य जैसी तकनीकों का उपयोग करने की क्षमता की आवश्यकता होती है। ऐसे कार्यों को हल करने से आप मुख्य अनुभागों के बारे में अपने ज्ञान का परीक्षण कर सकते हैं स्कूल पाठ्यक्रम, स्तर तर्कसम्मत सोच, प्रारंभिक अनुसंधान कौशल। यह कामअनुभागों में से एक को समर्पित है - एक मॉड्यूल वाले समीकरणों को हल करना। इसमें तीन अध्याय हैं। पहला अध्याय बुनियादी अवधारणाओं और सबसे महत्वपूर्ण सैद्धांतिक विचारों का परिचय देता है। दूसरा अध्याय एक मॉड्यूल वाले नौ मुख्य प्रकार के समीकरणों का प्रस्ताव करता है, उन्हें हल करने के तरीकों पर चर्चा करता है, और उदाहरणों की जांच करता है अलग - अलग स्तरकठिनाइयाँ। तीसरा अध्याय अधिक जटिल और गैर-मानक समीकरण (त्रिकोणमितीय, घातीय, लघुगणक और अपरिमेय) प्रस्तुत करता है। प्रत्येक प्रकार के समीकरण के लिए अभ्यास हैं स्वतंत्र निर्णय(उत्तर और निर्देश संलग्न हैं)। इस कार्य का मुख्य उद्देश्य शिक्षकों को पाठों की तैयारी और वैकल्पिक पाठ्यक्रमों के आयोजन में पद्धतिगत सहायता प्रदान करना है। सामग्री का उपयोग इस प्रकार भी किया जा सकता है शिक्षक का सहायकहाई स्कूल के छात्रों के लिए. कार्य में प्रस्तावित कार्य दिलचस्प हैं और हल करना हमेशा आसान नहीं होता है, जो आपको करने की अनुमति देता है सीखने की प्रेरणाछात्रों को अधिक जागरूक बनाने, उनकी क्षमताओं का परीक्षण करने और विश्वविद्यालयों में प्रवेश के लिए स्कूल स्नातकों की तैयारी के स्तर में सुधार करने के लिए। प्रस्तावित अभ्यासों के एक विभेदित चयन में सामग्री में महारत हासिल करने के प्रजनन स्तर से रचनात्मक तक संक्रमण शामिल है, साथ ही गैर-मानक समस्याओं को हल करते समय अपने ज्ञान को कैसे लागू किया जाए यह सिखाने का अवसर भी शामिल है।

अध्याय 1 परिचय।

धारा 1. निरपेक्ष मूल्य का निर्धारण .

परिभाषा : किसी वास्तविक संख्या का निरपेक्ष मान (मापांक)। एएक गैर-ऋणात्मक संख्या कहलाती है: एया -एक। पद का नाम: │ ए │ प्रविष्टि इस प्रकार है: "संख्या ए का मापांक" या "संख्या ए का पूर्ण मान"

│ ए, यदि ए > 0

│a│ = │ 0, यदि a = 0 (1)

│ - और, यदि ए
उदाहरण: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

अभिव्यक्ति मॉड्यूल का विस्तार करें:

a) │x - 8│, यदि x > 12 b) │2x + 3│, यदि x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3

धारा 2. मूल गुण.

आइए निरपेक्ष मूल्य के मूल गुणों पर विचार करें। संपत्ति #1: विपरीत संख्याओं में समान मॉड्यूल होते हैं, अर्थात। │а│=│- а│आइए हम दिखाएँ कि समानता सत्य है। आइए संख्या की परिभाषा लिखें - ए : │- ए│= (2) आइए सेट (1) और (2) की तुलना करें। यह स्पष्ट है कि परिभाषाएँ सम्पूर्ण मूल्यनंबर एऔर - एमेल खाना। इस तरह, │а│=│- а│
निम्नलिखित गुणों पर विचार करते समय, हम स्वयं को उनके निरूपण तक ही सीमित रखेंगे, क्योंकि उनका प्रमाण इसमें दिया गया है संपत्ति #2: वास्तविक संख्याओं की एक सीमित संख्या के योग का निरपेक्ष मान पदों के निरपेक्ष मानों के योग से अधिक नहीं होता है: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ संपत्ति #3: दो वास्तविक संख्याओं के बीच अंतर का निरपेक्ष मान उनके निरपेक्ष मानों के योग से अधिक नहीं होता है: │а - в│ ≤│а│+│в│ संपत्ति #4: वास्तविक संख्याओं की एक सीमित संख्या के गुणनफल का निरपेक्ष मान कारकों के निरपेक्ष मानों के गुणनफल के बराबर होता है: │а·в│=│а│·│в│ संपत्ति #5: वास्तविक संख्याओं के भागफल का निरपेक्ष मान उनके निरपेक्ष मानों के भागफल के बराबर होता है:

धारा 3. किसी संख्या के मापांक की अवधारणा की ज्यामितीय व्याख्या।

प्रत्येक वास्तविक संख्या को संख्या रेखा पर एक बिंदु से जोड़ा जा सकता है, जो इस वास्तविक संख्या की एक ज्यामितीय छवि होगी। संख्या रेखा पर प्रत्येक बिंदु मूल बिंदु से उसकी दूरी के अनुरूप है, अर्थात। मूल बिंदु से दिए गए बिंदु तक खंड की लंबाई। इस दूरी को हमेशा एक गैर-नकारात्मक मान माना जाता है। इसलिए, संबंधित खंड की लंबाई किसी दिए गए वास्तविक संख्या के निरपेक्ष मान की ज्यामितीय व्याख्या होगी

प्रस्तुत ज्यामितीय चित्रण स्पष्ट रूप से संपत्ति संख्या 1 की पुष्टि करता है, अर्थात। विपरीत संख्याओं का मापांक बराबर होता है। यहां से समानता की वैधता आसानी से समझ में आती है: │х – а│= │а – x│. समीकरण │x│= m का समाधान, जहां m ≥ 0, अर्थात् x 1.2 = ± m, भी अधिक स्पष्ट हो जाता है। उदाहरण: 1) │х│= 4 x 1.2 = ± 4 2) │х - 3│= 1
एक्स 1.2 = 2; 4

धारा 4. फ़ंक्शन का ग्राफ़ y = │х│

इस फ़ंक्शन का डोमेन सभी वास्तविक संख्याएँ हैं।

धारा 5. कन्वेंशन.

भविष्य में, समीकरणों को हल करने के उदाहरणों पर विचार करते समय, निम्नलिखित का उपयोग किया जाएगा प्रतीक: (- सिस्टम का संकेत [- समग्रता का संकेत समीकरणों (असमानताओं) की एक प्रणाली को हल करते समय, प्रणाली में शामिल समीकरणों (असमानताओं) के समाधानों का प्रतिच्छेदन पाया जाता है। समीकरणों (असमानताओं) के एक सेट को हल करते समय, समीकरणों (असमानताओं) के सेट में शामिल समाधानों का संघ पाया जाता है।

अध्याय 2. मापांक वाले समीकरणों को हल करना।

इस अध्याय में हम एक या अधिक मॉड्यूल वाले समीकरणों को हल करने के लिए बीजगणितीय तरीकों को देखेंगे।

धारा 1. फॉर्म के समीकरण │F (x)│= m

इस प्रकार के समीकरण को सरलतम कहा जाता है। इसका एक समाधान है यदि और केवल यदि m ≥ 0. मापांक की परिभाषा के अनुसार, मूल समीकरण दो समीकरणों के एक सेट के बराबर है: │ एफ(x)│=एम
उदाहरण:
№1. समीकरण हल करें: │7х - 2│= 9


उत्तर: एक्स 1 = - 1; एक्स 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; एक्स 2 = -2 एक्स (एक्स + 3) = 0 एक्स 1 = 0; एक्स 2 = -3 उत्तर: मूलों का योग है - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 निरूपित करें x 2 = m, m ≥ 0 x = 0 ; ±√5 मी 2 - 5 मी + 4 = 0 मी = 1; 4 - दोनों मान शर्त को पूरा करते हैं m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 उत्तर: समीकरण के मूलों की संख्या 7. व्यायाम:
№1. समीकरण को हल करें और मूलों का योग बताएं: │х - 5│= 3 №2 . समीकरण को हल करें और छोटे मूल को इंगित करें: │x 2 + x│= 0 №3 . समीकरण को हल करें और बड़े मूल को इंगित करें: │x 2 – 5x + 4│= 4 №4 .समीकरण को हल करें और संपूर्ण मूल इंगित करें: │2x 2 – 7x + 6│= 1 №5 .समीकरण को हल करें और मूलों की संख्या बताएं: │x 4 – 13x 2 + 50│= 14

धारा 2. फॉर्म के समीकरण F(│х│) = m

बाईं ओर का फ़ंक्शन तर्क मापांक चिह्न के अंतर्गत है, और दाईं ओर चर से स्वतंत्र है। आइए इस प्रकार के समीकरणों को हल करने के दो तरीकों पर विचार करें। 1 तरीका:निरपेक्ष मान की परिभाषा के अनुसार, मूल समीकरण दो प्रणालियों के संयोजन के बराबर है। जिनमें से प्रत्येक में एक सबमॉड्यूलर अभिव्यक्ति पर एक शर्त लगाई गई है। एफ(│х│)=एम
चूँकि फलन F(│x│) परिभाषा के पूरे क्षेत्र में सम है, समीकरण F(x) = m और F(- x) = m के मूल विपरीत संख्याओं के जोड़े हैं। इसलिए, यह किसी एक प्रणाली को हल करने के लिए पर्याप्त है (इस तरह से उदाहरणों पर विचार करने पर, एक प्रणाली का समाधान दिया जाएगा)। विधि 2:एक नए वेरिएबल को पेश करने की विधि का अनुप्रयोग। इस मामले में, अंकन │x│= a पेश किया गया है, जहां a ≥ 0 है। यह विधिडिज़ाइन में कम विशाल।
उदाहरण: №1 . समीकरण को हल करें: 3x 2 – 4│x│= - 1 आइए एक नए चर के परिचय का उपयोग करें। आइए हम │x│= a को निरूपित करें, जहां a ≥ 0. हमें समीकरण 3a 2 - 4a + 1 = 0 D = 16 - 12 = 4 a 1 = 1 a 2 = 1/3 प्राप्त होता है, मूल चर पर लौटें: │ x│=1 और │х│= 1/3. प्रत्येक समीकरण की दो जड़ें होती हैं। उत्तर: एक्स 1 = 1; एक्स 2 = - 1; एक्स 3 = 1 / 3 ; एक्स 4 = - 1 / 3 . №2. समीकरण हल करें: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
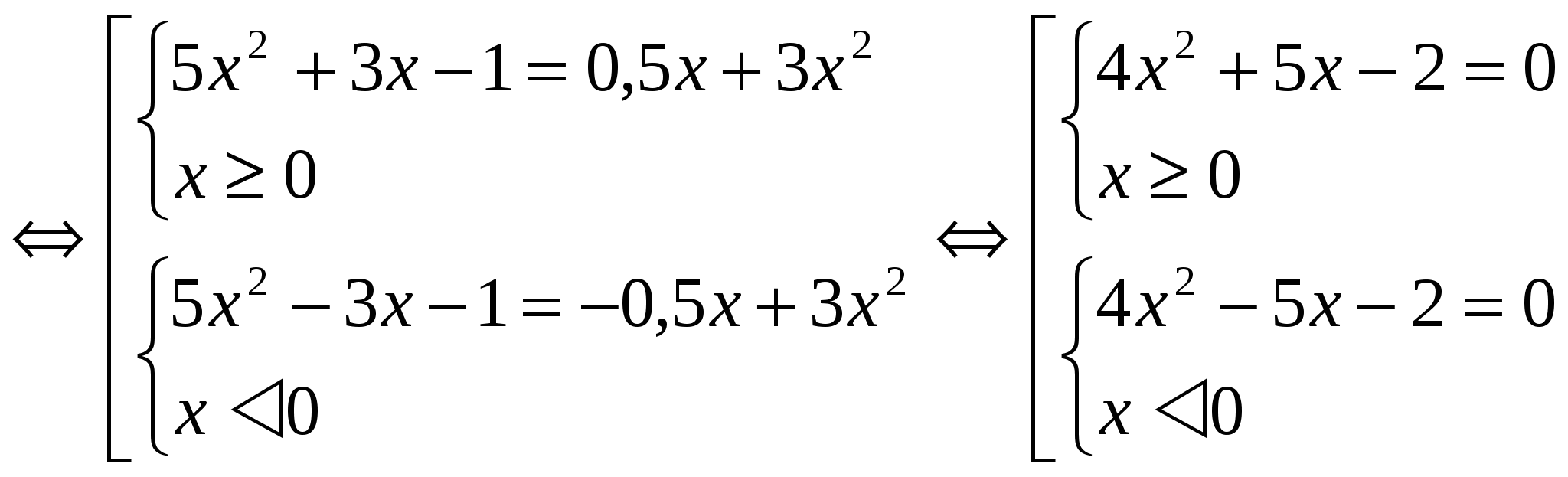आइए जनसंख्या की पहली प्रणाली का समाधान खोजें: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 ध्यान दें कि x 2 संतुष्ट नहीं करता है शर्त x ≥ 0. समाधान दूसरी प्रणाली मान x 1 के विपरीत संख्या होगी। उत्तर: एक्स 1 = -5+√57 / 8 ; एक्स 2 = 5-√57 / 8 .№3 . समीकरण को हल करें: x 4 – │х│= 0 आइए हम │х│= a को निरूपित करें, जहां a ≥ 0. हमें समीकरण मिलता है a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 मूल चर पर लौटें: │х│=0 और │х│= 1 x = 0; ± 1 उत्तर: एक्स 1 = 0; एक्स 2 = 1; एक्स 3 = - 1.
व्यायाम: №6. समीकरण हल करें: 2│х│ - 4.5 = 5 – 3 / 8 │х│ №7 . समीकरण को हल करें, अपने उत्तर में मूलों की संख्या बताएं: 3x 2 - 7│x│ + 2 = 0 №8 . समीकरण को हल करें, अपने उत्तर में पूर्णांक समाधान इंगित करें: x 4 + │x│ - 2 = 0

धारा 3. फॉर्म के समीकरण │F(x)│ = G(x)

इस प्रकार के समीकरण का दाहिना पक्ष एक चर पर निर्भर करता है और इसलिए, इसका समाधान केवल तभी होता है जब दाहिना पक्ष एक फ़ंक्शन G(x) ≥ 0 हो। मूल समीकरण को दो तरीकों से हल किया जा सकता है : 1 तरीका:मानक, इसकी परिभाषा के आधार पर एक मॉड्यूल के प्रकटीकरण पर आधारित है और इसमें दो प्रणालियों के संयोजन के बराबर संक्रमण शामिल है। │ एफ(x)│ =जी(एक्स)

फ़ंक्शन G(x) के लिए जटिल अभिव्यक्ति और फ़ंक्शन F(x) के लिए कम जटिल अभिव्यक्ति के मामले में इस पद्धति का तर्कसंगत रूप से उपयोग किया जा सकता है, क्योंकि यह माना जाता है कि फ़ंक्शन F(x) के साथ असमानताएं हल हो जाएंगी। विधि 2:एक समतुल्य प्रणाली में संक्रमण में शामिल होता है जिसमें दाईं ओर एक शर्त लगाई जाती है। │ एफ(एक्स)│= जी(एक्स)

यदि फ़ंक्शन G(x) के लिए अभिव्यक्ति फ़ंक्शन F(x) की तुलना में कम जटिल है, तो इस विधि का उपयोग करना अधिक सुविधाजनक है, क्योंकि असमानता G(x) ≥ 0 का समाधान इसके अलावा माना जाता है कई मॉड्यूलों में से, दूसरे विकल्प का उपयोग करने की अनुशंसा की जाती है। उदाहरण: №1. समीकरण हल करें: │x + 2│= 6 -2x
(1 रास्ता) उत्तर: एक्स = 1 1 / 3 №2.
│x 2 – 2x - 1│= 2 (x + 1)
(2 रास्ते) उत्तर: जड़ों का गुणनफल 3 है।
№3. समीकरण को हल करें और अपने उत्तर में मूलों का योग बताएं:
│x - 6│= x 2 - 5x + 9

उत्तर: मूलों का योग 4 है।
व्यायाम: №9. │x + 4│= - 3x №10. समीकरण को हल करें, अपने उत्तर में समाधानों की संख्या बताएं:│x 2 + x - 1│= 2x – 1 №11 . समीकरण को हल करें, अपने उत्तर में मूलों का गुणनफल बताएं:│x + 3│= x 2 + x – 6

धारा 4. फॉर्म के समीकरण │F(x)│= F(x) और │F(x)│= - F(x)

इस प्रकार के समीकरणों को कभी-कभी "सबसे सुंदर" कहा जाता है। चूंकि समीकरणों का दाहिना पक्ष चर पर निर्भर करता है, इसलिए समाधान तभी मौजूद होते हैं जब दाहिना पक्ष गैर-नकारात्मक हो। इसलिए, मूल समीकरण असमानताओं के बराबर हैं:
│F(x)│= F(x) F(x) ≥ 0 और │F(x)│= - F(x) F(x) उदाहरण: №1 . समीकरण को हल करें, अपने उत्तर में छोटे पूर्णांक मूल को इंगित करें: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0.6 उत्तर: एक्स = 1№2. समीकरण को हल करें, अपने उत्तर में अंतराल की लंबाई इंगित करें: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] उत्तर: अंतराल की लंबाई 6 है.№3 . समीकरण को हल करें और अपने उत्तर में पूर्णांक समाधानों की संख्या इंगित करें: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] उत्तर: 4 संपूर्ण समाधान.№4 . समीकरण को हल करें और अपने उत्तर में सबसे बड़ा मूल बताएं:
│4 – एक्स -
│= 4 – एक्स –
x 2 – 5x + 5 = 0 डी = 5 x 1.2 =
≈ 1,4

उत्तर: एक्स = 3.

व्यायाम: №12. समीकरण को हल करें, उत्तर में संपूर्ण मूल इंगित करें: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. समीकरण को हल करें, अपने उत्तर में पूर्णांक समाधानों की संख्या इंगित करें: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. अपने उत्तर में समीकरण को हल करें, एक पूर्णांक इंगित करें जो समीकरण का मूल नहीं है:

धारा 5. फॉर्म के समीकरण │F(x)│= │G(x)│

चूँकि समीकरण के दोनों पक्ष गैर-नकारात्मक हैं, समाधान में दो मामलों पर विचार करना शामिल है: सबमॉड्यूलर अभिव्यक्तियाँ चिह्न में समान या विपरीत हैं। इसलिए, मूल समीकरण दो समीकरणों के संयोजन के बराबर है: │ एफ(एक्स)│= │ जी(एक्स)│
उदाहरण: №1. समीकरण को हल करें, अपने उत्तर में संपूर्ण मूल इंगित करें: │x + 3│=│2x - 1│
उत्तर: संपूर्ण मूल x = 4.№2. प्रश्न हल करें: │ x – x 2 - 1│=│2x – 3 – x 2 │
उत्तर: एक्स = 2.№3 . समीकरण को हल करें और अपने उत्तर में जड़ों का गुणनफल इंगित करें:




मूल समीकरण 4x 2 + 2x – 1 = 0 x 1.2 = - 1±√5 / 4 उत्तर: जड़ों का गुणनफल - 0.25 है। व्यायाम: №15 . समीकरण को हल करें और अपने उत्तर में संपूर्ण समाधान इंगित करें: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. समीकरण को हल करें, अपने उत्तर में छोटे मूल को इंगित करें:│5x - 3│=│7 - x│ №17 . समीकरण को हल करें और अपने उत्तर में मूलों का योग बताएं:

धारा 6. गैर-मानक समीकरणों को हल करने के उदाहरण

इस खंड में हम गैर-मानक समीकरणों के उदाहरणों पर विचार करेंगे, जिन्हें हल करने पर अभिव्यक्ति का निरपेक्ष मान परिभाषा द्वारा प्रकट होता है। उदाहरण:

№1. समीकरण को हल करें, अपने उत्तर में मूलों का योग बताएं: x · │x│- 5x – 6 = 0
उत्तर: मूलों का योग 1 होता है №2. . समीकरण को हल करें, अपने उत्तर में छोटे मूल को इंगित करें: x 2 - 4x ·
- 5 = 0
उत्तर: छोटी जड़ x = - 5. №3. प्रश्न हल करें:

उत्तर: x = -1. व्यायाम: №18. समीकरण को हल करें और मूलों का योग बताएं: x · │3x + 5│= 3x 2 + 4x + 3
№19. समीकरण हल करें: x 2 – 3x =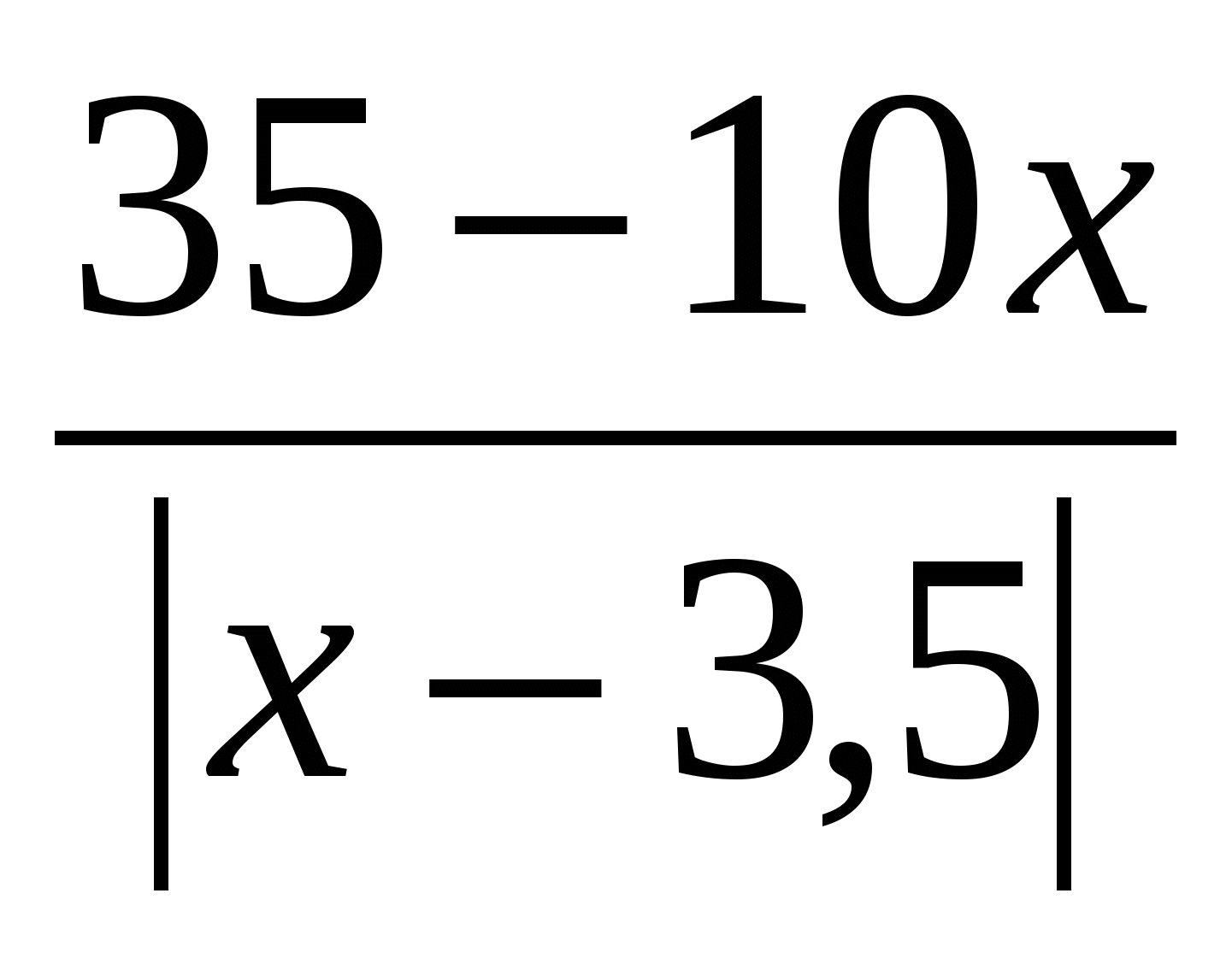

№20. प्रश्न हल करें:

धारा 7. फॉर्म के समीकरण │F(x)│+│G(x)│=0

यह नोटिस करना आसान है कि इस प्रकार के समीकरण के बाईं ओर गैर-नकारात्मक मात्राओं का योग है। इसलिए, मूल समीकरण का कोई हल तभी है जब दोनों पद एक ही समय में शून्य के बराबर हों। समीकरण समीकरणों की प्रणाली के बराबर है: │ एफ(एक्स)│+│ जी(एक्स)│=0
उदाहरण: №1 . प्रश्न हल करें:
उत्तर: एक्स = 2. №2. प्रश्न हल करें: उत्तर: एक्स = 1. व्यायाम: №21. प्रश्न हल करें: №22 . समीकरण को हल करें और अपने उत्तर में मूलों का योग बताएं: №23 . समीकरण को हल करें और अपने उत्तर में समाधानों की संख्या बताएं:

धारा 8. फॉर्म के समीकरण │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m

इस प्रकार के समीकरणों को हल करने के लिए अंतराल विधि का प्रयोग किया जाता है। यदि हम इसे मॉड्यूल के क्रमिक विस्तार द्वारा हल करते हैं, तो हमें मिलता है एनप्रणालियों का सेट, जो बहुत बोझिल और असुविधाजनक है। आइए अंतराल विधि एल्गोरिदम पर विचार करें: 1). परिवर्तनीय मान खोजें एक्स, जिसके लिए प्रत्येक मॉड्यूल शून्य के बराबर है (सबमॉड्यूलर अभिव्यक्तियों का शून्य):
2). पाए गए मानों को एक संख्या रेखा पर अंकित करें, जो अंतरालों में विभाजित है (अंतरालों की संख्या क्रमशः बराबर है)। एन+1 ) 3). निर्धारित करें कि प्रत्येक परिणामी अंतराल पर प्रत्येक मॉड्यूल किस चिह्न से प्रकट होता है (समाधान करते समय, आप एक संख्या रेखा का उपयोग कर सकते हैं, उस पर चिह्नों को चिह्नित कर सकते हैं) 4)। मूल समीकरण समुच्चय के समतुल्य है एन+1 सिस्टम, जिनमें से प्रत्येक में चर की सदस्यता इंगित की गई है एक्सअंतरालों में से एक. उदाहरण: №1 . समीकरण को हल करें और अपने उत्तर में सबसे बड़ा मूल बताएं:
1). आइए सबमॉड्यूलर अभिव्यक्तियों के शून्य खोजें: x = 2; एक्स = -3 2). आइए पाए गए मानों को संख्या रेखा पर चिह्नित करें और निर्धारित करें कि परिणामी अंतराल पर प्रत्येक मॉड्यूल किस चिह्न से प्रकट होता है:
एक्स - 2 एक्स - 2 एक्स - 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- कोई समाधान नहीं समीकरण के दो मूल हैं। उत्तर: सबसे बड़ा मूल x = 2. №2. समीकरण को हल करें और अपने उत्तर में संपूर्ण मूल प्रदान करें:
1). आइए सबमॉड्यूलर अभिव्यक्तियों के शून्य खोजें: x = 1.5; एक्स = - 1 2). आइए पाए गए मानों को संख्या रेखा पर चिह्नित करें और निर्धारित करें कि परिणामी अंतराल पर प्रत्येक मॉड्यूल किस चिह्न से प्रकट होता है: x + 1 x + 1 x + 1 - + +
-1 1.5 x 2x – 3 2x – 3 2x – 3 - - +
3).
अंतिम प्रणाली का कोई समाधान नहीं है, इसलिए समीकरण की दो जड़ें हैं। समीकरण को हल करते समय, आपको दूसरे मॉड्यूल के सामने "-" चिह्न पर ध्यान देना चाहिए। उत्तर: संपूर्ण मूल x = 7. №3. समीकरण को हल करें, अपने उत्तर में मूलों का योग बताएं: 1). आइए सबमॉड्यूलर अभिव्यक्तियों के शून्य खोजें: x = 5; एक्स = 1; एक्स = - 2 2). आइए पाए गए मानों को संख्या रेखा पर चिह्नित करें और निर्धारित करें कि परिणामी अंतराल पर प्रत्येक मॉड्यूल किस चिह्न से प्रकट होता है: x - 5 x - 5 x - 5 x - 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
समीकरण के दो मूल x = 0 और 2 हैं। उत्तर: मूलों का योग 2 है। №4 . समीकरण हल करें: 1). आइए सबमॉड्यूलर अभिव्यक्तियों के शून्य खोजें: x = 1; एक्स = 2; एक्स = 3. 2). आइए हम यह निर्धारित करें कि प्रत्येक मॉड्यूल परिणामी अंतराल पर किस चिन्ह से प्रकट होता है। 3).
आइए पहले के समाधानों को संयोजित करें तीन प्रणालियाँ. उत्तर: ; एक्स = 5.
व्यायाम: №24. प्रश्न हल करें:
№25. समीकरण को हल करें और अपने उत्तर में मूलों का योग बताएं: №26. समीकरण को हल करें और अपने उत्तर में छोटे मूल को इंगित करें: №27. समीकरण को हल करें और अपने उत्तर में बड़े मूल को इंगित करें:

धारा 9. कई मॉड्यूल वाले समीकरण

एकाधिक मॉड्यूल वाले समीकरण सबमॉड्यूलर अभिव्यक्तियों में निरपेक्ष मानों की उपस्थिति मानते हैं। इस प्रकार के समीकरणों को हल करने का मूल सिद्धांत "बाहरी" से शुरू होने वाले मॉड्यूल का क्रमिक प्रकटीकरण है। समाधान के दौरान, अनुभाग संख्या 1, संख्या 3 में चर्चा की गई तकनीकों का उपयोग किया जाता है।

उदाहरण: №1. प्रश्न हल करें:
उत्तर: एक्स = 1; - ग्यारह। №2. प्रश्न हल करें:
उत्तर: एक्स = 0; 4; - 4. №3. समीकरण को हल करें और अपने उत्तर में जड़ों का गुणनफल इंगित करें:
उत्तर: जड़ों का गुणनफल है - 8. №4. प्रश्न हल करें:
आइए हम जनसंख्या के समीकरणों को निरूपित करें (1) और (2) और डिज़ाइन में आसानी के लिए उनमें से प्रत्येक के समाधान पर अलग से विचार करें। चूंकि दोनों समीकरणों में एक से अधिक मॉड्यूल शामिल हैं, इसलिए सिस्टम के सेट में समतुल्य संक्रमण करना अधिक सुविधाजनक है। (1)

(2)


उत्तर:
व्यायाम: №36. समीकरण को हल करें, अपने उत्तर में जड़ों का योग इंगित करें: 5 │3x-5│ = 25 x №37. समीकरण को हल करें, यदि एक से अधिक मूल हैं, तो अपने उत्तर में मूलों का योग इंगित करें: │x + 2│ x – 3x – 10 = 1 №38. समीकरण हल करें: 3 │2x -4│ = 9 │x│ №39. समीकरण को हल करें और अपने उत्तर में जड़ों की संख्या इंगित करें: 2 │ पाप x│ = √2 №40 . समीकरण को हल करें और अपने उत्तर में जड़ों की संख्या बताएं:

धारा 3. लघुगणकीय समीकरण।

निम्नलिखित समीकरणों को हल करने से पहले, लघुगणक और लघुगणक फ़ंक्शन के गुणों की समीक्षा करना आवश्यक है। उदाहरण: №1. समीकरण को हल करें, अपने उत्तर में जड़ों के उत्पाद को इंगित करें: लॉग 2 (x+1) 2 + लॉग 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

स्थिति 1: यदि x ≥ - 1, तो लघुगणक 2 (x+1) 2 + लघुगणक 2 (x+1) = 6 लघुगणक 2 (x+1) 3 = लघुगणक 2 2 6 (x+1) 3 = 2 6 x+1 = 4 2 (-(x+1)) = 6 लघुगणक 2 (-(x+1) 3) = लघुगणक 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – शर्त x-1 को संतुष्ट करता है
उत्तर: जड़ों का गुणनफल है - 15.
№2. समीकरण को हल करें, अपने उत्तर में मूलों का योग बताएं: lg
ओ.डी.जेड.

उत्तर: मूलों का योग 0.5 है।
№3. समीकरण हल करें: लॉग 5
ओ.डी.जेड.

उत्तर: x = 9. №4. समीकरण हल करें: │2 + log 0.2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 आइए दूसरे आधार पर जाने के लिए सूत्र का उपयोग करें। │2 - लघुगणक 5 x│+ 3 = │1 + लघुगणक 5 x│
│2 - लॉग 5 x│- │1 + लॉग 5 x│= - 3 आइए सबमॉड्यूलर अभिव्यक्तियों के शून्य खोजें: x = 25; x = ये संख्याएँ स्वीकार्य मानों की सीमा को तीन अंतरालों में विभाजित करती हैं, इसलिए समीकरण तीन प्रणालियों के एक सेट के बराबर है।
उत्तर: )